��Ŀ����
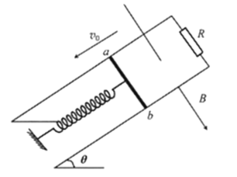
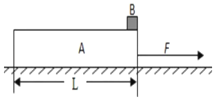
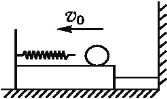
����Ŀ����ͼ��ʾ���⻬ˮƽ������һ��ľ�壬��ľ����ϱ���Ҳ��ˮƽ�⻬�ģ��Ҷ���ϸ��˩��ǽ�ϣ�����ϲ��̶�һ���ʵ��ɣ�����Ϊm=1kg��������ijһ���ٶ�v0(δ֪)��ľ����ϱ��������������˶��������뵯�ɸսӴ�ʱ���ӱ�����С����ٶ�������ٶ���ͬ�����ɱ�ѹ����������ٶ���С�����ٶȼ�С�����ٶȵ�һ��ʱ�����ɵĵ�������Ϊ3J����ʱϸ��ǡ�ñ�����(��������һ�����е�������ʧ)���˺�ľ�忪ʼ�����˶���
��1������ʼ�˶�ʱ�ij��ٶ��Ƕ��٣�
��2����ľ�������MΪ1kg��ľ�忪ʼ�˶��ɵĵ�����������Ƕ��٣�
��3��Ϊʹľ���õĶ������ľ�������ӦΪ���
���𰸡���1��2![]() m/s����2��3.5J����3��M=
m/s����2��3.5J����3��M=![]() m
m
��������
(1)���뵯����ɵ�ϵͳ�����غ㣬�������غ㶨�ɵã�
![]()
��ã�
![]() =2
=2![]() m/s
m/s
(2)����ľ����ɵ�ϵͳ�����غ㣬�ɶ����غ㶨�ɵã�
m![]() v0��(m+M)v
v0��(m+M)v
�������غ㶨�ɵã�
E+![]() m(
m(![]() v0)2��
v0)2��![]() (m+M)v2+Em
(m+M)v2+Em
��ã����ɵ���������ܣ�
Em��![]() =3.5J
=3.5J
(3)������ľ����ɵ�ϵͳ�������غ㣺
m![]() v0��Mv1
v0��Mv1
�����غ㣺
E+![]() m(
m(![]() v0)2��
v0)2��![]() Mv12
Mv12
���ľ��������
m=4M
��
![]()

��ϰ��ϵ�д�
�����Ŀ