题目内容
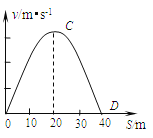
【题目】质量为50kg的运动员，在一座高桥上做“蹦极”运动。他所用的弹性绳自由长度为12m,假设弹性绳中的弹力与弹性绳的伸长量之间的关系遵循胡克定律，在整个运动中弹性绳不超过弹性限度。运动员从桥面下落，能到达距桥面为40m的最低点D处，运动员下落速率
跟下落距离S的关系如图所示，运动员在C点时的速度最大。空气阻力不计，重力加速度g取10m/s2。求
（1）弹性绳的劲度系数
；
（2）运动员到达D点时，弹性绳的弹性势能
；
（3）运动员到达D点时的加速度值
。
【答案】（1）
（2）
(3) 
【解析】试题分析：（1）在C点速度最大，则C点是平衡位置，则有重力等于弹力，结合胡克定律即可求解；（2）对由O到D的过程运用机械能守恒定律列式即可求解；（3）在D点，由胡克定律求得弹簧的弹力，再根据牛顿第二定律求加速度．
（1）运动员在C点受到的弹力与重力大小相等，合外力为0，加速度为0，所以速度最大．
则
代入数据得
（2）运动员到达D点的速率为0，在整个下落过程中减少的重力势能全部转化为弹簧增加的弹性势能
代入数据得： 
（3）在D点弹簧的弹
根据牛顿第二定律： 
联立解得： 
练习册系列答案
阅读快车系列答案
相关题目
