题目内容
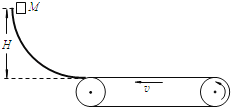
【题目】小明同学在上海迪士尼乐园体验了超刺激的游戏项目“创极速光轮”后，对“过山车”类型的轨道运动充满了兴趣。为此他自己利用器材设计拼接了一条轨道，如图所示，ABC为一条水平轨道，BC段长度为20cm，斜直轨道CD段长度15cm，与水平面夹角θ=370，BC段与CD段在C点平滑连接，竖直圆弧轨道DEF的圆心为O1，半径R1=10cm，圆轨道与CD相切于D点，E为圆弧轨道的最高点，半径O1F水平，FG段为竖直轨道，与1/4圆轨道GH相切于G点，圆形轨道GH圆心为O2，半径R2=4cm，G、O2、D在同一水平线上，水平轨道HK长度为40cm，HK与CD轨道错开。在AB段的A端固定一轻质弹簧，弹簧自然伸长时刚好位于B端，现在B端放置一个小环（可视为质点）但不栓接，小环的质量为m=0.01kg，现推动小环压缩弹簧d后释放，小环恰好能运动到D点。已知小环只在轨道BC、CD、HK上受到摩擦力，动摩擦因数μ=0.5，弹簧弹性势能与弹簧弹性形变量的二次方成正比。不计空气阻力，sin37°=0.6，cos37°=0.8，g=10m/s2.则：
（1）求小环在B点的速度大小v；
（2）某次实验，弹簧压缩量为2d，求小环在E处对轨道的压力；
（3）小环能否停在HK上？若能，求出弹簧压缩量的取值范围；若不能，请说明理由。
【答案】（1）
m/s （2）1.04N 方向竖直向上（3）小环不能停在HK上
【解析】（1）由B到D，根据动能定理： 
，
代入数据得：v=
m/s；
（2）弹簧压缩量为d时， 
， 弹簧压缩量为2d时， 
在B的动能变为原来的4倍，速度
，设到E点速度为vE，轨道对环的弹力为FE，根据动能定理：
联立解得：FE=1.04N
根据牛顿第三定律，小环在E处对轨道的压力为1.04N，方向竖直向上；
（3）假设小环在E点速度为零，在HK上滑行的距离为x，根据动能定理：
带入数据得：x=0.44m>0.4m，小环不能停在HK上。
