题目内容
2.如图甲所示,在一个正方形金属线圈区域内,存在着磁感应强度B随时间变化的匀强磁场,磁场的方向与线圈平面垂直.金属线圈所围的面积S=100cm2,匝数n=1000,线圈电阻r=2.0Ω.线圈与电阻R构成闭合回路,电阻R=8.0Ω.匀强磁场的磁感应强度随时间变化的情况如图乙所示,求: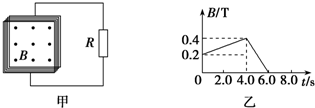
(1)0~4.0s内通过电阻R的感应电流大小;
(2)0~6.0s内整个闭合电路中产生的热量.
分析 (1)由图读出磁通量的变化率,根据法拉第电磁感应定律求出感应电动势,由欧姆定律求解感应电流的大小.
(2)根据焦耳定律分别求出0~4.0s时间内和4.0s~6.0s时间内的热量,再求总和.
解答 解:(1)根据法拉第电磁感应定律,0~4.0 s时间内线圈中磁通量均匀变化,感应电动势E1=n$\frac{△{∅}_{1}}{△{t}_{1}}$=n$\frac{△{B}_{1}}{△{t}_{1}}•S$
根据闭合电路欧姆定律,闭合回路中的感应电流:I1=$\frac{E}{R+r}$
代入数据,解得:I1=0.05 A;
(2)由图象可知,在4.0~6.0 s时间内,线圈中产生的感应电动势E2=n$\frac{△{∅}_{2}}{△{t}_{2}}$=n$\frac{{∅}_{6}-{∅}_{4}}{△{t}_{2}}$
根据闭合电路欧姆定律,t=5.0 s时闭合回路中的感应电流I2=$\frac{{E}_{2}}{R+r}$=0.2 A
根据焦耳定律,在0~4.0 s内闭合电路中产生的热量Q1=I12(r+R)△t1=0.1 J
在4.0~6.0 s内闭合电路中产生的热量Q2=I22(r+R)△t2=0.8 J
那么0~6.0 s内闭合电路中产生的热量 Q=Q1+Q2=0.9J.
答:(1)0~4.0s内通过电阻R的感应电流大小0.05 A;
(2)0~6.0s内整个闭合电路中产生的热量0.9J.
点评 本题是电磁感应与电路知识简单的综合.当穿过回路的磁通量均匀变化时,回路中产生恒定电流,可以用焦耳定律求解热量.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
2. 如图所示,a、b为两个固定的带等量正电荷的点电荷,虚线ab、cd互相垂直平分,负电荷q由c点从静止释放,如只受电场力作用,则下列关于此电荷运动的说法正确的是( )
如图所示,a、b为两个固定的带等量正电荷的点电荷,虚线ab、cd互相垂直平分,负电荷q由c点从静止释放,如只受电场力作用,则下列关于此电荷运动的说法正确的是( )
 如图所示,a、b为两个固定的带等量正电荷的点电荷,虚线ab、cd互相垂直平分,负电荷q由c点从静止释放,如只受电场力作用,则下列关于此电荷运动的说法正确的是( )
如图所示,a、b为两个固定的带等量正电荷的点电荷,虚线ab、cd互相垂直平分,负电荷q由c点从静止释放,如只受电场力作用,则下列关于此电荷运动的说法正确的是( )| A. | 从c到d速度一直增大 | |
| B. | 在cd间做往复运动,经O点时速度最大 | |
| C. | 从c到O加速度减小,从O到d加速度增大 | |
| D. | 若在c点给q一个合适的初速度,它可以做匀速圆周运动 |
13.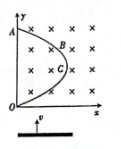 如图所示,在xOy平面内存在磁感应强度B=2T的匀强磁场,OA与OCA为固定于垂直平面内的光滑金属导轨,其中OCA满足曲线方程x=0.5sin$\frac{π}{5}$y(m),C点的横坐标最大,导轨OA与OCA相交处的O点与A点分别接有体积可忽略的定值电阻R1=6Ω和R2=12Ω(图中未画出).现有一长L=0.5m、质量m=0.1kg的金属棒在竖直向上的外力作用下,以v=2m/s的速度沿导轨向上匀速运动.棒与两导轨接触良好,除电阻R1、R2外其余电阻不计,取g=10m/s2.下列判断正确的是( )
如图所示,在xOy平面内存在磁感应强度B=2T的匀强磁场,OA与OCA为固定于垂直平面内的光滑金属导轨,其中OCA满足曲线方程x=0.5sin$\frac{π}{5}$y(m),C点的横坐标最大,导轨OA与OCA相交处的O点与A点分别接有体积可忽略的定值电阻R1=6Ω和R2=12Ω(图中未画出).现有一长L=0.5m、质量m=0.1kg的金属棒在竖直向上的外力作用下,以v=2m/s的速度沿导轨向上匀速运动.棒与两导轨接触良好,除电阻R1、R2外其余电阻不计,取g=10m/s2.下列判断正确的是( )
 如图所示,在xOy平面内存在磁感应强度B=2T的匀强磁场,OA与OCA为固定于垂直平面内的光滑金属导轨,其中OCA满足曲线方程x=0.5sin$\frac{π}{5}$y(m),C点的横坐标最大,导轨OA与OCA相交处的O点与A点分别接有体积可忽略的定值电阻R1=6Ω和R2=12Ω(图中未画出).现有一长L=0.5m、质量m=0.1kg的金属棒在竖直向上的外力作用下,以v=2m/s的速度沿导轨向上匀速运动.棒与两导轨接触良好,除电阻R1、R2外其余电阻不计,取g=10m/s2.下列判断正确的是( )
如图所示,在xOy平面内存在磁感应强度B=2T的匀强磁场,OA与OCA为固定于垂直平面内的光滑金属导轨,其中OCA满足曲线方程x=0.5sin$\frac{π}{5}$y(m),C点的横坐标最大,导轨OA与OCA相交处的O点与A点分别接有体积可忽略的定值电阻R1=6Ω和R2=12Ω(图中未画出).现有一长L=0.5m、质量m=0.1kg的金属棒在竖直向上的外力作用下,以v=2m/s的速度沿导轨向上匀速运动.棒与两导轨接触良好,除电阻R1、R2外其余电阻不计,取g=10m/s2.下列判断正确的是( )| A. | 当金属棒运动到C点时,感应电动势最大且为1V | |
| B. | 金属棒在导轨上运动时,R2上消耗的最大功率为$\frac{1}{3}$W | |
| C. | 外力F的最大值为1.5N | |
| D. | 在金属棒滑过导轨OCA的过程中,整个回路产生的热量为1.25J |
17.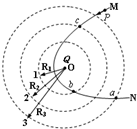 如图所示,在O点固定一点电荷Q,一带电粒子P从很远处以初速度v0射入电场,MN为粒子仅在电场力作用下的运动轨迹.虚线是以O为中心,R1、R2、R3为半径画出的三个圆,且R2-R1=R3-R2,a、b、c为轨迹MN与三个圆的3个交点,以下说法正确的是( )
如图所示,在O点固定一点电荷Q,一带电粒子P从很远处以初速度v0射入电场,MN为粒子仅在电场力作用下的运动轨迹.虚线是以O为中心,R1、R2、R3为半径画出的三个圆,且R2-R1=R3-R2,a、b、c为轨迹MN与三个圆的3个交点,以下说法正确的是( )
 如图所示,在O点固定一点电荷Q,一带电粒子P从很远处以初速度v0射入电场,MN为粒子仅在电场力作用下的运动轨迹.虚线是以O为中心,R1、R2、R3为半径画出的三个圆,且R2-R1=R3-R2,a、b、c为轨迹MN与三个圆的3个交点,以下说法正确的是( )
如图所示,在O点固定一点电荷Q,一带电粒子P从很远处以初速度v0射入电场,MN为粒子仅在电场力作用下的运动轨迹.虚线是以O为中心,R1、R2、R3为半径画出的三个圆,且R2-R1=R3-R2,a、b、c为轨迹MN与三个圆的3个交点,以下说法正确的是( )| A. | P、Q两电荷可能同号,也可能异号 | |
| B. | a点电势大于b点电势 | |
| C. | P在a的电势能大于在c点的电势能 | |
| D. | P由c点到b点的动能变化大于由c点到a点的动能变化 |
7.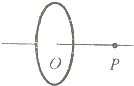 如图所示,一固定的半径为R的圆环均匀带点,将一带电量为q=-1×10-3C的试探电荷从无穷远(电势能为零)处移至圆环轴线上的O点时,电场力对该试探电荷所做的功为4×10-3J,再将其从O点移到P点时,需克服电场力做功1×10-3J,则( )
如图所示,一固定的半径为R的圆环均匀带点,将一带电量为q=-1×10-3C的试探电荷从无穷远(电势能为零)处移至圆环轴线上的O点时,电场力对该试探电荷所做的功为4×10-3J,再将其从O点移到P点时,需克服电场力做功1×10-3J,则( )
 如图所示,一固定的半径为R的圆环均匀带点,将一带电量为q=-1×10-3C的试探电荷从无穷远(电势能为零)处移至圆环轴线上的O点时,电场力对该试探电荷所做的功为4×10-3J,再将其从O点移到P点时,需克服电场力做功1×10-3J,则( )
如图所示,一固定的半径为R的圆环均匀带点,将一带电量为q=-1×10-3C的试探电荷从无穷远(电势能为零)处移至圆环轴线上的O点时,电场力对该试探电荷所做的功为4×10-3J,再将其从O点移到P点时,需克服电场力做功1×10-3J,则( )| A. | 圆环带负电 | |
| B. | 电场中P点的电势为3V | |
| C. | 试探电荷在该电场的P点所具有的电势能为3×10-3J | |
| D. | OP间的电势差为-1V |
14.在“探究滑块速度随时间变化的规律”实验中,某研究性学习小组在一端装有定滑轮的长木板的中段粘上均匀的薄砂纸,砂面朝上,还选用了质量为100g的长方体木块、一段较长的棉绳、一盒钩码(单个质量为50g)、电磁打点计时器、纸带、复写纸、学生电源和导线若干,实验装置如图甲所示,实验时在小车上加载四个钩码,在棉绳的右端悬挂三个钩码,接通电源,释放小车,成功打出了一条纸带,纸带的局部如图乙,大部分点的时刻和速度的对应关系已经描绘在图丙里.

(1)根据图乙,请计算0.20s时刻点的瞬时速度,填入下表中.
(2)根据上述表格中的五组数据,请在图丙中描绘出对应的五个点,再根据图中所有的点,描绘出最能反映出木块运动性质的v-t图象.
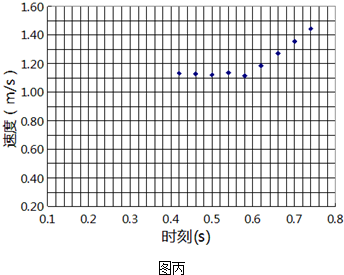
(3)根据上述图象,请说明滑块的运动性质:滑块先做匀加速运动,接着做匀速运动,最后再做匀加速运动
(4)在实验结束后,同学们对实验进行了反思:A同学认为本实验有必要在左端垫上小垫块以平衡摩擦力,B同学认为没有必要,你认为B的观点正确; C同学认为本实验中三个钩码质量太大,有必要换质量更小的配重,以满足“重物质量m远小于滑块质量M”这一条件,D同学认为没有必要,你认为D的观点正确;同学们都认为可以由实验数据粗略计算出木块与砂纸之间的动摩擦因数,其值为0.50(保留两位有效数字).

(1)根据图乙,请计算0.20s时刻点的瞬时速度,填入下表中.
| 时刻(s) | 0.20 | 0.24 | 0.28 | 0.32 | 0.36 |
| 速度(m/s) | 0.68 | 0.75 | 0.87 | 0.93 | 1.01 |

(3)根据上述图象,请说明滑块的运动性质:滑块先做匀加速运动,接着做匀速运动,最后再做匀加速运动
(4)在实验结束后,同学们对实验进行了反思:A同学认为本实验有必要在左端垫上小垫块以平衡摩擦力,B同学认为没有必要,你认为B的观点正确; C同学认为本实验中三个钩码质量太大,有必要换质量更小的配重,以满足“重物质量m远小于滑块质量M”这一条件,D同学认为没有必要,你认为D的观点正确;同学们都认为可以由实验数据粗略计算出木块与砂纸之间的动摩擦因数,其值为0.50(保留两位有效数字).
11.在某段电路中,其两端电压为U,通过电路电流为I,通电时间为t,关于电功和电热说法正确的是( )
| A. | 在任何电路中,电功UIt等于电热I2Rt | |
| B. | 在任何电路中,电功等于UIt,电热等于I2Rt | |
| C. | 在纯电阻电路中,电功大于电热 | |
| D. | 电流通过电动机时,电动机工作的电功等于电热 |
12.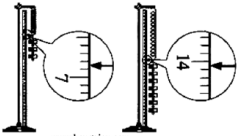 某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L2.
某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L2.
①下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是L5和L6.测量记录表:
②实验中,L3和L7两个值还没有测定,请你根据上图将这两个测量值填入记录表中.
③为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm、d2=L5-L1=6.90cm、d3=L6-L3=7.00,请你给出第四个差值:dA=L7-L3=7.20cm.
④根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=$\frac{({d}_{1}+{d}_{2}+{d}_{3}+{d}_{4})}{4×4}$,代入数据解得:△L=1.75cm.
⑤计算弹簧的劲度系数k=28N/m.(g取9.8m/s2)
 某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L2.
某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L2.①下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是L5和L6.测量记录表:
| 代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值/cm | 1.70 | 3.40 | 5.10 | 8.60 | 10.3 | 12.1 |
③为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm、d2=L5-L1=6.90cm、d3=L6-L3=7.00,请你给出第四个差值:dA=L7-L3=7.20cm.
④根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=$\frac{({d}_{1}+{d}_{2}+{d}_{3}+{d}_{4})}{4×4}$,代入数据解得:△L=1.75cm.
⑤计算弹簧的劲度系数k=28N/m.(g取9.8m/s2)