题目内容
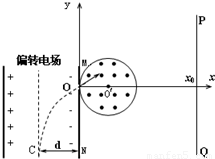
如图所示,在平面坐标系xOy内,同种带正电离子,质量m=1.0×10-20kg、带电量q=1.0×10-10C,以相同速度不断从C点垂直射入匀强电场,偏转后通过极板MN上的小孔O离开电场时的速度大小为v=2.0×106m/s,方向与x轴成30°角斜向上.在y轴右侧有一个圆心位于O'(0.01m,0)点,半径r=0.01m的圆形磁场区域,磁场方向垂直纸面向外,磁感应强度B=0.01T,有一垂直于x轴的面积足够大的竖直荧光屏PQ置于坐标x=0.04m处.已知NC之间的距离d=0.02m.试求:(1)粒子在磁场中的运动轨迹半径;
(2)偏转电场强度的大小;
(3)若圆形磁场区可沿x轴移动,圆心O'在x轴上的移动范围为(0.01m,+∞),由于磁场位置的不同,导致粒子打在荧光屏上的位置也不同,求粒子打在荧光屏上点的纵坐标的范围.
【答案】分析:(1)离子在磁场中做匀速圆周运动,由洛仑兹力提供向心力,由牛顿第二定律求轨迹半径;
(2)粒子射入电场后做类平抛运动,将速度v分解为沿x轴和y轴两个方向,得到初速度,根据动能定理求场强E;
(3)由几何知识分析并求解离子打在荧光屏的最低点和最高点的纵坐标,即得到纵坐标的范围.
解答:解:(1)离子在磁场中做匀速圆周运动,由于洛仑兹力提供向心力,则有:qvB=m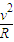 ①
①
解得:R=0.02m
(2)将速度v分解为如图所示的x方向速度v1和y方向速度v2,
得到:v2=vsin30°=0.5v ②
则初速度为v=vc ③
离子在偏转电场中,由动能定理:Eqd= mv2-
mv2- mv
mv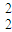 ④
④
联立②③④解得:E=7.5×103V/m
(3)当圆心O′在x=0.01m时,由于R=0.02m=2r,所以离子从x轴上的D点离开磁场.
由几何关系可知,离子打在荧光屏的最低点,纵坐标为:y1=-(x-2r)tan30°=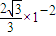 m ⑤
m ⑤
随着磁场向右移动,荧光屏上亮点的位置逐渐向上移动,当速度v的方向与磁场边界相切时,离子将打在荧光屏的最高位置.其最高点的纵坐标为:
y2=xtan30°=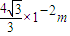 ⑥
⑥
故离子打在荧光屏上的点纵坐标范围为[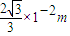 ,
,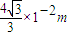 ]
]
答:
(1)粒子在磁场中的运动轨迹半径为0.02m;
(2)偏转电场强度的大小为7.5×103V/m;
(3)粒子打在荧光屏上点的纵坐标范围为[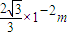 ,
,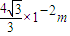 ].
].
点评:本题是带电粒子在复合场中运动的问题,磁场中由牛顿第二定律求轨迹半径,由几何知识求相关距离是常用的方法.电场中运用运动的分解法和动能定理处理此类问题.
(2)粒子射入电场后做类平抛运动,将速度v分解为沿x轴和y轴两个方向,得到初速度,根据动能定理求场强E;
(3)由几何知识分析并求解离子打在荧光屏的最低点和最高点的纵坐标,即得到纵坐标的范围.
解答:解:(1)离子在磁场中做匀速圆周运动,由于洛仑兹力提供向心力,则有:qvB=m
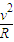 ①
①解得:R=0.02m
(2)将速度v分解为如图所示的x方向速度v1和y方向速度v2,
得到:v2=vsin30°=0.5v ②
则初速度为v=vc ③
离子在偏转电场中,由动能定理:Eqd=
 mv2-
mv2- mv
mv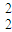 ④
④联立②③④解得:E=7.5×103V/m
(3)当圆心O′在x=0.01m时,由于R=0.02m=2r,所以离子从x轴上的D点离开磁场.
由几何关系可知,离子打在荧光屏的最低点,纵坐标为:y1=-(x-2r)tan30°=
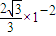 m ⑤
m ⑤随着磁场向右移动,荧光屏上亮点的位置逐渐向上移动,当速度v的方向与磁场边界相切时,离子将打在荧光屏的最高位置.其最高点的纵坐标为:
y2=xtan30°=
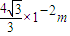 ⑥
⑥故离子打在荧光屏上的点纵坐标范围为[
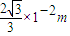 ,
,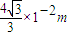 ]
]答:
(1)粒子在磁场中的运动轨迹半径为0.02m;
(2)偏转电场强度的大小为7.5×103V/m;
(3)粒子打在荧光屏上点的纵坐标范围为[
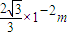 ,
,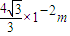 ].
].点评:本题是带电粒子在复合场中运动的问题,磁场中由牛顿第二定律求轨迹半径,由几何知识求相关距离是常用的方法.电场中运用运动的分解法和动能定理处理此类问题.

练习册系列答案
相关题目
 (2011?合肥模拟)如图所示,在平面坐标系xoy内,第II、III象限内存在沿y轴正方向的匀强电场,电场强度大小为E,第I、IV象限内存在磁场方向垂直于纸面向外的匀强磁场.一带正电的粒子从第III象限中的Q(-2L,-L)点以速度v0沿x轴正方向射出,恰好从坐标原点O进人磁场,然后又从y轴上的P(-2L,0)点射出磁场.不计粒子重力,求:
(2011?合肥模拟)如图所示,在平面坐标系xoy内,第II、III象限内存在沿y轴正方向的匀强电场,电场强度大小为E,第I、IV象限内存在磁场方向垂直于纸面向外的匀强磁场.一带正电的粒子从第III象限中的Q(-2L,-L)点以速度v0沿x轴正方向射出,恰好从坐标原点O进人磁场,然后又从y轴上的P(-2L,0)点射出磁场.不计粒子重力,求: (2011?海南模拟)如图所示,在xoy坐标平面的第一象限内有一沿y轴负方向的匀强电场,在第四象限内有一垂直于平面向外的匀强磁场,一质量为m,带电量为+q的粒子(重力不计)经过电场中坐标为(3L,L)的P点时的速度大小为V0.方向沿x轴负方向,然后以与x轴负方向成45°角进入磁场,最后从坐标原点O射出磁场求:
(2011?海南模拟)如图所示,在xoy坐标平面的第一象限内有一沿y轴负方向的匀强电场,在第四象限内有一垂直于平面向外的匀强磁场,一质量为m,带电量为+q的粒子(重力不计)经过电场中坐标为(3L,L)的P点时的速度大小为V0.方向沿x轴负方向,然后以与x轴负方向成45°角进入磁场,最后从坐标原点O射出磁场求: 如图所示,在xOy坐标的第一象限内分布有垂直xOy平面向外的匀强磁场,磁感应强度大小为B=2.5×10-2T.在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线垂直y轴),极板间距d=0.4m,极板与左侧电路相连接,通过移动滑动头P可以改变极板MN间的电压.a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压
如图所示,在xOy坐标的第一象限内分布有垂直xOy平面向外的匀强磁场,磁感应强度大小为B=2.5×10-2T.在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线垂直y轴),极板间距d=0.4m,极板与左侧电路相连接,通过移动滑动头P可以改变极板MN间的电压.a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压 如图所示,在平面坐标xoy内,在y轴左侧与直线x=-2L右侧区域内存在沿y轴正方向的匀强电场,在y轴右侧存在一矩形匀强磁场区域,磁场方向垂直坐标平面向外(图中未画出),坐标原点O为磁场边界上一点,一带电粒子从电场边界上Q(-2L,-L)点以速度v0沿x轴正方向射入电场,并恰好从坐标原点O进入磁场,在磁场中作半径为
如图所示,在平面坐标xoy内,在y轴左侧与直线x=-2L右侧区域内存在沿y轴正方向的匀强电场,在y轴右侧存在一矩形匀强磁场区域,磁场方向垂直坐标平面向外(图中未画出),坐标原点O为磁场边界上一点,一带电粒子从电场边界上Q(-2L,-L)点以速度v0沿x轴正方向射入电场,并恰好从坐标原点O进入磁场,在磁场中作半径为 如图所示,在平面直角中,有方向平行于坐标平面的匀强电场,已测得坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,那么电场强度的大小为E=
如图所示,在平面直角中,有方向平行于坐标平面的匀强电场,已测得坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,那么电场强度的大小为E=