题目内容
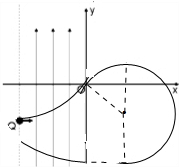
 如图所示,在平面坐标xoy内,在y轴左侧与直线x=-2L右侧区域内存在沿y轴正方向的匀强电场,在y轴右侧存在一矩形匀强磁场区域,磁场方向垂直坐标平面向外(图中未画出),坐标原点O为磁场边界上一点,一带电粒子从电场边界上Q(-2L,-L)点以速度v0沿x轴正方向射入电场,并恰好从坐标原点O进入磁场,在磁场中作半径为
如图所示,在平面坐标xoy内,在y轴左侧与直线x=-2L右侧区域内存在沿y轴正方向的匀强电场,在y轴右侧存在一矩形匀强磁场区域,磁场方向垂直坐标平面向外(图中未画出),坐标原点O为磁场边界上一点,一带电粒子从电场边界上Q(-2L,-L)点以速度v0沿x轴正方向射入电场,并恰好从坐标原点O进入磁场,在磁场中作半径为| 2 |
(1)粒子经过O点时速度的大小和方向;
(2)电场强度与磁感应强度大小之比;
(3)粒子由Q点到P点所用的时间.
分析:(1)粒子做类平抛运动,根据分位移公式列式求解两个分速度,合成得到合速度的大小和方向;
(2)先对粒子的类平抛运动根据分位移公式列式;再对粒子的匀速圆周运动过程根据牛顿第二定律列式,最后联立求解即可;
(3)粒子在电场中是类似平抛运动,在磁场中是匀速圆周运动,最后垂直y轴返回电场区域,故矩形磁场区域与坐标轴不平行;根据t=
T求解磁场中的运动时间,运用正交分解法求解电场中的运动时间,最后求和即可.
(2)先对粒子的类平抛运动根据分位移公式列式;再对粒子的匀速圆周运动过程根据牛顿第二定律列式,最后联立求解即可;
(3)粒子在电场中是类似平抛运动,在磁场中是匀速圆周运动,最后垂直y轴返回电场区域,故矩形磁场区域与坐标轴不平行;根据t=
| θ |
| 360° |
解答:解:(1)粒子在电场中做类平抛运动,根据分位移公式,有:
x方向:2L=v0t
y方向:L=
t
解得:vy=v0
故离开电场时的合速度:v=
=
v0,与x轴成45°斜向右上方;
(2)粒子在电场中做类平抛运动,根据分位移公式,有:
x方向:2L=v0t
y方向:L=
?
?t2
解得:E=
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律,有:
qvB=m
其中:r=
L
B=
=
=
故:
=
=
(3)粒子在电场中是类似平抛运动,在磁场中是匀速圆周运动,轨迹如图:
粒子Q到O的时间为:t1=
粒子由O到离开磁场的时间:t2=
T=
T
其中:T=
=
故:t2=
×
=
粒子返回电场后是平抛运动,根据其水平分运动得到:
t3=
=
=
故粒子由Q点到P点所用的时间为:
t=t1+t2+t3=
+
+
=(8+6
+5π)
答:(1)粒子经过O点时速度的大小为
v0,与x轴成45°斜向右上方;
(2)电场强度与磁感应强度大小之比为
;
(3)粒子由Q点到P点所用的时间为(8+6
+5π)
.
x方向:2L=v0t
y方向:L=
| 0+vy |
| 2 |
解得:vy=v0
故离开电场时的合速度:v=
|
| 2 |
(2)粒子在电场中做类平抛运动,根据分位移公式,有:
x方向:2L=v0t
y方向:L=
| 1 |
| 2 |
| qE |
| m |
解得:E=
m
| ||
| 2qL |
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律,有:
qvB=m
| v2 |
| r |
其中:r=
| 2 |
B=
| mv |
| qr |
m?
| ||
q?
|
| mv0 |
| qL |
故:
| E |
| B |
| ||||
|
| v0 |
| 2 |
(3)粒子在电场中是类似平抛运动,在磁场中是匀速圆周运动,轨迹如图:

粒子Q到O的时间为:t1=
| 2L |
| v0 |
粒子由O到离开磁场的时间:t2=
| 225° |
| 360° |
| 5 |
| 8 |
其中:T=
| 2πm |
| qB |
| 2πL |
| v0 |
故:t2=
| 5 |
| 8 |
| 2πL |
| v0 |
| 5πL |
| 4v0 |
粒子返回电场后是平抛运动,根据其水平分运动得到:
t3=
| 2L+r?sin45° |
| v |
2L+
| ||||||
|
3
| ||
| 2 |
| L |
| v0 |
故粒子由Q点到P点所用的时间为:
t=t1+t2+t3=
| 2L |
| v0 |
| 5πL |
| 4v0 |
3
| ||
| 2 |
| L |
| v0 |
| 2 |
| L |
| 4v0 |
答:(1)粒子经过O点时速度的大小为
| 2 |
(2)电场强度与磁感应强度大小之比为
| v0 |
| 2 |
(3)粒子由Q点到P点所用的时间为(8+6
| 2 |
| L |
| 4v0 |
点评:本题关键明确粒子的运动规律,然后分类平抛运动和匀速圆周运动分段考虑,类似平抛运动是根据分位移公式列式求解,匀速圆周运动是根据牛顿第二定律列式,不难.

练习册系列答案
相关题目
 (2011?合肥模拟)如图所示,在平面坐标系xoy内,第II、III象限内存在沿y轴正方向的匀强电场,电场强度大小为E,第I、IV象限内存在磁场方向垂直于纸面向外的匀强磁场.一带正电的粒子从第III象限中的Q(-2L,-L)点以速度v0沿x轴正方向射出,恰好从坐标原点O进人磁场,然后又从y轴上的P(-2L,0)点射出磁场.不计粒子重力,求:
(2011?合肥模拟)如图所示,在平面坐标系xoy内,第II、III象限内存在沿y轴正方向的匀强电场,电场强度大小为E,第I、IV象限内存在磁场方向垂直于纸面向外的匀强磁场.一带正电的粒子从第III象限中的Q(-2L,-L)点以速度v0沿x轴正方向射出,恰好从坐标原点O进人磁场,然后又从y轴上的P(-2L,0)点射出磁场.不计粒子重力,求: (2011?海南模拟)如图所示,在xoy坐标平面的第一象限内有一沿y轴负方向的匀强电场,在第四象限内有一垂直于平面向外的匀强磁场,一质量为m,带电量为+q的粒子(重力不计)经过电场中坐标为(3L,L)的P点时的速度大小为V0.方向沿x轴负方向,然后以与x轴负方向成45°角进入磁场,最后从坐标原点O射出磁场求:
(2011?海南模拟)如图所示,在xoy坐标平面的第一象限内有一沿y轴负方向的匀强电场,在第四象限内有一垂直于平面向外的匀强磁场,一质量为m,带电量为+q的粒子(重力不计)经过电场中坐标为(3L,L)的P点时的速度大小为V0.方向沿x轴负方向,然后以与x轴负方向成45°角进入磁场,最后从坐标原点O射出磁场求: 如图所示,在xOy坐标的第一象限内分布有垂直xOy平面向外的匀强磁场,磁感应强度大小为B=2.5×10-2T.在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线垂直y轴),极板间距d=0.4m,极板与左侧电路相连接,通过移动滑动头P可以改变极板MN间的电压.a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压
如图所示,在xOy坐标的第一象限内分布有垂直xOy平面向外的匀强磁场,磁感应强度大小为B=2.5×10-2T.在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线垂直y轴),极板间距d=0.4m,极板与左侧电路相连接,通过移动滑动头P可以改变极板MN间的电压.a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压 如图所示,在平面直角中,有方向平行于坐标平面的匀强电场,已测得坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,那么电场强度的大小为E=
如图所示,在平面直角中,有方向平行于坐标平面的匀强电场,已测得坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,那么电场强度的大小为E=