��Ŀ����
 ��2011?����ģ�⣩��ͼ��ʾ����xoy����ƽ��ĵ�һ��������һ��y�Ḻ�������ǿ�糡���ڵ�����������һ��ֱ��ƽ���������ǿ�ų���һ����Ϊm��������Ϊ+q�����ӣ��������ƣ������糡������Ϊ��3L��L����P��ʱ���ٶȴ�СΪV0��������x�Ḻ����Ȼ������x�Ḻ�����45��ǽ���ų�����������ԭ��O����ų���
��2011?����ģ�⣩��ͼ��ʾ����xoy����ƽ��ĵ�һ��������һ��y�Ḻ�������ǿ�糡���ڵ�����������һ��ֱ��ƽ���������ǿ�ų���һ����Ϊm��������Ϊ+q�����ӣ��������ƣ������糡������Ϊ��3L��L����P��ʱ���ٶȴ�СΪV0��������x�Ḻ����Ȼ������x�Ḻ�����45��ǽ���ų�����������ԭ��O����ų�����1����ǿ�糡�ij�ǿE�Ĵ�С��
��2����ǿ�ų��ĴŸ�Ӧǿ��B�Ĵ�С��
��3�����Ӵ�P���˶���ԭ��O���õ�ʱ�䣮
��������1�������Ӵ�P�㴹ֱ����糡������ƽ���˶���������x���45�㴹ֱ������ǿ�ų�������������������������Բ���˶������Ŵ�ԭ��������������ڵ糡P����ٶȿ�����ս���ų����ٶȣ����ɶ��ܶ����ɵõ糡ǿ�ȣ�
��2���Ӷ�����ƽ���˶���Բ���˶���ϼ��ι�ϵ�����Բ����Ӧ�İ뾶����˿�����Ÿ�Ӧǿ�ȣ�
��3��ͬʱ�����ڹ�ʽ���˶�ѧ��ʽ��������Ӵ�P�㵽O���ʱ�䣮
��2���Ӷ�����ƽ���˶���Բ���˶���ϼ��ι�ϵ�����Բ����Ӧ�İ뾶����˿�����Ÿ�Ӧǿ�ȣ�
��3��ͬʱ�����ڹ�ʽ���˶�ѧ��ʽ��������Ӵ�P�㵽O���ʱ�䣮
����⣺�����ڵ糡�о�����P������ƽ���˶�������ų���������Բ���˶�����O������������˶��켣��ͼ��ʾ��
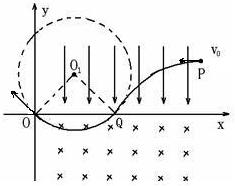 ��1����������O��ʱ���ٶȴ�СΪv��OQ��ΪԲ�ܣ�PQ��Ϊ�����ߣ����ݶԳ��Կ�֪��������Q��ʱ���ٶȴ�СҲΪv��������x���������45��ǣ��ɵã�V0=vcos45��
��1����������O��ʱ���ٶȴ�СΪv��OQ��ΪԲ�ܣ�PQ��Ϊ�����ߣ����ݶԳ��Կ�֪��������Q��ʱ���ٶȴ�СҲΪv��������x���������45��ǣ��ɵã�V0=vcos45��
��ã�v=
v0
�����Ӵ�P�˶���Q�Ĺ����У��ɶ��ܶ����ã�
-qE0L=
m
-
mv2
��ã�E0=
��2������ǿ�糡��P��Q�Ĺ����У�
ˮƽ�����λ��Ϊx=v0t1
��ֱ�����λ��Ϊy=
t1=L
�ɵ�XQP=2L��OQ=L
��OQ=2Rcos45���������QO��Բ���˶��İ뾶��R=
L
��R=
��B0=
��
��3����Q��ʱ��vy=v0tan45��=v0
�����Ӵ�P��Q����ʱ��Ϊt1������ֱ�������У�t1=
=
���Ӵ�Q���˶���O���õ�ʱ��Ϊ��t2=
T=
�����Ӵ�O���˶���P�����õ�ʱ��Ϊ��t��=t1+t2=
+
=
�𣺣�1����ǿ�糡�ij�ǿE�Ĵ�СΪ
��
��2����ǿ�ų��ĴŸ�Ӧǿ��B�Ĵ�СΪ
��
��3�����Ӵ�P���˶���ԭ��O���õ�ʱ��
��
 ��1����������O��ʱ���ٶȴ�СΪv��OQ��ΪԲ�ܣ�PQ��Ϊ�����ߣ����ݶԳ��Կ�֪��������Q��ʱ���ٶȴ�СҲΪv��������x���������45��ǣ��ɵã�V0=vcos45��
��1����������O��ʱ���ٶȴ�СΪv��OQ��ΪԲ�ܣ�PQ��Ϊ�����ߣ����ݶԳ��Կ�֪��������Q��ʱ���ٶȴ�СҲΪv��������x���������45��ǣ��ɵã�V0=vcos45�� ��ã�v=
| 2 |
�����Ӵ�P�˶���Q�Ĺ����У��ɶ��ܶ����ã�
-qE0L=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
��ã�E0=
m
| ||
| 2qL |
��2������ǿ�糡��P��Q�Ĺ����У�
ˮƽ�����λ��Ϊx=v0t1
��ֱ�����λ��Ϊy=
| v0 |
| 2 |
�ɵ�XQP=2L��OQ=L
��OQ=2Rcos45���������QO��Բ���˶��İ뾶��R=
| ||
| 2 |
��R=
| mv |
| Bq |
��B0=
| 2mv0 |
| qL |
��3����Q��ʱ��vy=v0tan45��=v0
�����Ӵ�P��Q����ʱ��Ϊt1������ֱ�������У�t1=
| L | ||
|
| 2L |
| v0 |
���Ӵ�Q���˶���O���õ�ʱ��Ϊ��t2=
| 90�� |
| 360�� |
| ��L |
| 4v0 |
�����Ӵ�O���˶���P�����õ�ʱ��Ϊ��t��=t1+t2=
| 2L |
| v0 |
| ��L |
| 4v0 |
| (8+��)L |
| 4v0 |
�𣺣�1����ǿ�糡�ij�ǿE�Ĵ�СΪ
m
| ||
| 2qL |
��2����ǿ�ų��ĴŸ�Ӧǿ��B�Ĵ�СΪ
| 2mv0 |
| qL |
��3�����Ӵ�P���˶���ԭ��O���õ�ʱ��
| (8+��)L |
| 4v0 |
������������������ڵ糡����һ���ٶ�����ƽ���˶�������һ���ٶȽ�����ǿ�ų���������Բ���˶����糡��������������������������������û����������ƽ���˶����˶��ĺϳ���ֽ����������Բ���˶��ص���������뾶����֪���ȵĹ�ϵ��

��ϰ��ϵ�д�
 �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
�����Ŀ
 ��2011?����ģ�⣩��ͼ��ʾ��A��BΪ�����̶��ĵ�����ͬ������ɣ����������ߵ��е㴦��һ�����������˶��������C���ָ����Cһ����ֱ�����ߵij��ٶ�v0�������Ƶ��C���ܵ�����������ڵ��C�˶������е��ٶȺͼ��ٶ����������˵����ȷ���ǣ�������
��2011?����ģ�⣩��ͼ��ʾ��A��BΪ�����̶��ĵ�����ͬ������ɣ����������ߵ��е㴦��һ�����������˶��������C���ָ����Cһ����ֱ�����ߵij��ٶ�v0�������Ƶ��C���ܵ�����������ڵ��C�˶������е��ٶȺͼ��ٶ����������˵����ȷ���ǣ������� ��2011?����ģ�⣩��ͼ��ʾ�������ֱ�ΪmA��mB��A��B��������������ӷ������Ϊ�ȵ�б���ϣ���ʼ��ƽ����б�����ϵ�����F��A��ʹ������б���ȼ���������A��B��б��Ķ�Ħ��������Ϊ�̣�Ϊ�����������ϵ����������еİ취�ǣ�������
��2011?����ģ�⣩��ͼ��ʾ�������ֱ�ΪmA��mB��A��B��������������ӷ������Ϊ�ȵ�б���ϣ���ʼ��ƽ����б�����ϵ�����F��A��ʹ������б���ȼ���������A��B��б��Ķ�Ħ��������Ϊ�̣�Ϊ�����������ϵ����������еİ취�ǣ������� ��2011?����ģ�⣩��ͼ��ʾ��Բ�����A�����һ����ΪM��С����P��ʹԲ���建������ת��������P��A��ת��A��㣬�����������Pʼ����Բ���屣����Ծ�ֹ����ôP���ܾ�Ħ����f�Ĵ�С��ʱ��t�ı仯�����ǣ�������
��2011?����ģ�⣩��ͼ��ʾ��Բ�����A�����һ����ΪM��С����P��ʹԲ���建������ת��������P��A��ת��A��㣬�����������Pʼ����Բ���屣����Ծ�ֹ����ôP���ܾ�Ħ����f�Ĵ�С��ʱ��t�ı仯�����ǣ������� ��2011?����ģ�⣩��ͼ��ʾ�Ǽס����������ͬһ��������˶�ͼ����ͼ����Կ�����0��4���ڣ�������
��2011?����ģ�⣩��ͼ��ʾ�Ǽס����������ͬһ��������˶�ͼ����ͼ����Կ�����0��4���ڣ������� ��2011?����ģ�⣩һ������Ȧ������ǿ�ų��У����1s�ڴŸ��ߴ�ֱ��Ȧƽ�棨����ֱ��ֽ�棩�����ͼ����ʾ���Ÿ�Ӧǿ����ʱ��仯�Ĺ�ϵ��ͼ����ʾ����ô���ڵ�2s����Ȧ�и�Ӧ����I�������ܰ�����F���ж���ȷ���ǣ�������
��2011?����ģ�⣩һ������Ȧ������ǿ�ų��У����1s�ڴŸ��ߴ�ֱ��Ȧƽ�棨����ֱ��ֽ�棩�����ͼ����ʾ���Ÿ�Ӧǿ����ʱ��仯�Ĺ�ϵ��ͼ����ʾ����ô���ڵ�2s����Ȧ�и�Ӧ����I�������ܰ�����F���ж���ȷ���ǣ�������