��Ŀ����
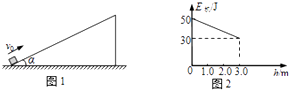
����Ŀ����ͼ��ʾ������mB=3.5kg������Bͨ��һ�ᵯ�ɹ����ڵ����ϣ����ɵľ���ϵ��k=100N/m��һ����һ��������B���ӣ��ƹ���Ħ������������С������O1��O2����һ�������ڹ⻬ֱ�˶��˵ġ�����mA=1.6kg��С��A���ӣ���ֱ֪�˹̶����˳�LΪ0.8m������ˮƽ��ļнǦ�=37�㣮��ʼʱʹС��A��ֹ��������A�����������ӱ���ˮƽ����ʱ�����е�����FΪ45N����֪AO1=0.5m���������ٶ�gȡ10m/s2 �� ���Ӳ����쳤���ֽ�С��A�Ӿ�ֹ�ͷţ���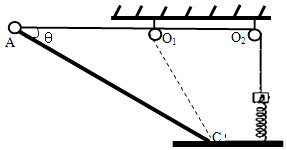
��1�����ͷ�С��A֮ǰ���ɵ��α�����
��2����С��A�˶�����C��ʱ���ٶȣ�
���𰸡�
��1���⣺�ͷ�С��ǰ��B���ھ�ֹ״̬�������������������������ʵ��ɱ����죬�赯���α���Ϊx�У�
kx=F��mBg
���x=0.1m
�����ͷ�С��A֮ǰ���ɵ��α���Ϊ0.1m
��2���⣺������֪���˳�L=0.8m���ʡ�ACO1=��=37���CO1=AO1����A����Cʱ�����ɵ����������״̬��ȣ�����B�ֻص�ԭλ�ã���C���A���ٶ���ƽ�������ʹ�ֱ������������зֽ⣬
�ɵã�ƽ������������ٶȼ�ΪB���ٶȣ��ɼ��ι�ϵ�ã�vB'=vA��cos37��
���������½������ɻ�е���غ�ã�mAgLsin37��= ![]() mAvA'2+
mAvA'2+ ![]() mB vB'2������ã�vA'=2m/s
mB vB'2������ã�vA'=2m/s
����С��A�˶�����C��ʱ���ٶ�Ϊ2m/s
����������1�����ݺ��˶��ɣ�ֱ����ʽ��⼴�ɡ�
��2��С���»������У������е���غ㣬�����ٶȵĺϳɺͷֽ��ϼ��ι�ϵ������ٶȣ������û�е���غ㶨���з�����⡣
�����㾫�����������⣬������Ҫ�˽��е���غ㼰������(��ֻ���������͵��ɵ����������������£����嶯�ܺ��������ܣ����������ܣ������ת��������е�ܵ��������ֲ���)��

 ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�