题目内容
【题目】如图所示,一足够长且不可伸长的柔软轻绳跨过光滑轻定滑轮,绳两端各系一小球a和b,a球静置于地面,并用手托住b球,使轻绳刚好绷紧,此时b球距地面高度h=0.6m.由静止释放b球,在b球着地前的瞬间,a球立即与轻绳脱离.已知mb=2ma , g取10m/s2 , 不计空气阻力.求: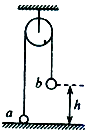
(1)b球着地时的速度大小;
(2)a球从开始脱离轻绳至再次回到地面的时间.
【答案】
(1)
解:b下落的过程,对小球a和b,由系统的机械能守恒得:
mbgh=magh+ ![]() (ma+mb)v2
(ma+mb)v2
代入数据得:v=2m/s
(2)
解:a球脱离轻绳后做竖直上抛运动,可以看成一种匀减速直线运动,取竖直向上为正方向,小球a落地时通过的位移为﹣h,由运动学规律得:
﹣h=vt﹣ ![]() gt2
gt2
解得:t=0.6s,(t=﹣0.2s舍去)
【解析】(1)对ab整体,受力分析可知,由于只有重力做功,系统的机械能守恒,由对统由机械能守恒定律列式可以求得结果.(2)a球脱离轻绳后做竖直上抛运动,可以看成一种匀减速直线运动,由位移时间公式求解时间.
【考点精析】本题主要考查了机械能守恒及其条件和机械能综合应用的相关知识点,需要掌握在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变;系统初态的总机械能E 1 等于末态的总机械能E 2 ,即E1 =E2;系统减少的总重力势能ΔE P减 等于系统增加的总动能ΔE K增 ,即ΔE P减 =ΔE K增;若系统只有A、

练习册系列答案
相关题目