Question

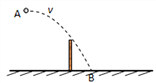
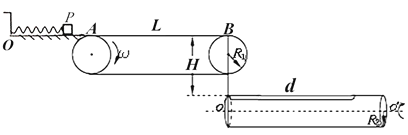
【题目】如图所示，光滑水平面OA与水平传送带相切于A点，传送带的水平部分AB长m，转动轮半径m。一水平放置、半径m的薄壁圆柱筒绕轴匀速转动，筒壁上自左端处开始有一与轴线平行、长度m的长槽，圆筒左端面和B点在同一竖直面上，顶端距B点m，且小滑块P的速度方向和圆筒轴线在同一竖直面上。已知小滑块P（可视为质点，以下简称P）的质量kg，与传送带间的动摩擦因数，取m/s2，现让P压缩弹簧，则：

（1）若传送带保持静止，为使得P能到达B点，弹簧弹性势能至少多大；

（2）若P能从B点飞离传送带，飞离时长槽恰好转动到圆筒的正下方，且P能进入长槽，求圆筒周期；

（3）若P滑上A点时 m/s，为使P能从B点飞离传送带，从长槽进入后又从长槽穿出（假设圆筒周期满足条件），整个过程不与圆筒相撞，传送带转动轮的角速度应满足什么条件。

Answer 1

【答案】（1）11J；（2）s（n=0,1,2,3……）（3） rad/s

【解析】（1）由功能关系可知，

解得：Ep=11 J

（2）从B点飞出到圆筒上端

根据圆筒匀速转动周期性可知： （n=0,1,2,3……）

解得： s（n=0,1,2,3……）

（3）小滑块P能从C点飞离需满足： ，得到： m/s

设小滑块P从C点下落到下端位置的时间：

则小球能从长槽顺利穿出需满足条件： 即 m/s

假设小滑块P在AB上全程匀减速有：

假设小滑块P在AB上全程匀加速有：

m/s m/s

分析可知全程匀减速的末速度 ,

所以转动轮的角速度最小值为0

全程匀加速的末速度 ，

所以转动轮的角速度最大值为 rad/s

综上分析可得： rad/s