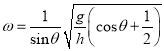题目内容
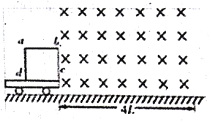
【题目】如图所示，A为一固定在地面上的光滑弧形轨道，质量为2m的足够长的小车B紧靠弧形轨道的右侧静止在水平光滑地面上，弧形轨道末端的切线水平且恰好在小车的上表面，一质量为m的滑块C自弧形轨道的a点由静止开始下滑，当滑块C与小车相对静止时，它们的速度为
，滑块相对于小车的滑行距离为d，滑块与小车的动摩擦因数为μ，重力加速度为g，滑块C可视为质点，从滑块开始下滑到滑块与小车相对静止的过程中，下列判断正确的是（ ）
A. 小车对滑块的摩擦力做功等于μmgd
B. 系统损失的机械能为μmgd
C. 滑块C到达弧形轨道末端时速度为
D. a点与弧形轨道末端的竖直高度为
【答案】BD
【解析】滑块C以v滑上小车，在摩擦力作用下减速，最后与小车共速，滑块动能减少，转化为小车的动能和热量，而系统产生的热量
，而滑块C相对小车的位移为
，故系统产生的热量为
，故小车对滑块的摩擦力做的功大于
，故A错误；根据能量守恒定律可知，系统损失的机械能等于，故B正确；滑块C滑上小车，系统动量守恒，则有：
，解得：
，故C错误；滑块C从弧形下滑时机械能守恒，则有：
，解得：
，故D正确，故选BD.
练习册系列答案
相关题目
