题目内容
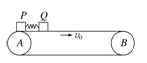
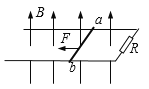
【题目】如图所示，一轻弹簧的一端与竖直墙壁相连，另一端与放在光滑水平面上的长木板左端接触，轻弹簧处于原长，长木板的质量为M，一质量为m的物块以一定的初速度从长木板的右端向左滑上长木板。已知物块与长木板间的动摩擦因数为 μ，轻弹簧的劲度系数为k，在长木板向左运动的过程中，物块始终在木板上相对木板向左滑动，求：
（1）物块滑上长木板的瞬间， 长木板的加速度大小；
（2）长木板向左运动的最大速度。
【答案】（1）
（2）
【解析】（1）物块刚滑上木板瞬间，木板所受摩擦力大小f=μN
N=mg
对木板，由牛顿第二定律得：f=Ma
联立解得木板此时的加速度：
（2）设长木板速度最大时弹簧的压缩距离为x ，此时弹簧的弹力：F=kx
长木板速度最大时：F=f
在此过程中弹簧对木板做功：
对木板，根据动能定理有： fx-W=
Mv2
联立解得：
练习册系列答案
相关题目
