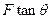题目内容
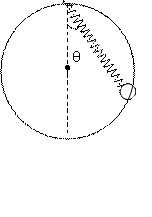
一轻绳通过无摩擦的定滑轮在倾角为30°的光滑斜面上的物体m1连接,另一端和套在竖直光滑杆上的物体m2连接.已知定滑轮到杆的距离为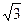 m.物体m2由静止从AB连线为水平位置开始下滑1 m时,m1、m2恰受力平衡如图5-10所示.试求:
m.物体m2由静止从AB连线为水平位置开始下滑1 m时,m1、m2恰受力平衡如图5-10所示.试求:
(1)m2在下滑过程中的最大速度.
(2)m2沿竖直杆能够向下滑动的最大距离.
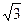 m.物体m2由静止从AB连线为水平位置开始下滑1 m时,m1、m2恰受力平衡如图5-10所示.试求:
m.物体m2由静止从AB连线为水平位置开始下滑1 m时,m1、m2恰受力平衡如图5-10所示.试求:(1)m2在下滑过程中的最大速度.
(2)m2沿竖直杆能够向下滑动的最大距离.

(1)2.15 m/s,(2)2.31 m
(1)由图可知,随m2的下滑,绳子拉力的竖直分量是逐渐增大的,m2在C点受力恰好平衡,因此m2从B到C是加速过程,以后将做减速运动,所以m2的最大速度即出现在图示位置.对m1、m2组成的系统来说,在整个运动过程中只有重力和绳子拉力做功,但绳子拉力做功代数和为零,所以系统机械能守恒.ΔE增=ΔE减,即
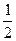 m1v12+
m1v12+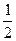 m22v2+m1g(A
m22v2+m1g(A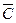 -A
-A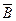 )sin30°=m2g·B
)sin30°=m2g·B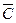
又由图示位置m1、m2受力平衡,应有:
Tcos∠ACB=m2g,T=m1gsin30°
又由速度分解知识知v1=v2cos∠ACB,代入数值可解得v2="2.15" m/s,
(2)m2下滑距离最大时m1、m2速度为零,在整个过程中应用机械能守恒定律,得:
ΔE增′=ΔE减′
即:m1g(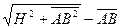 )sin30°=m2gH
)sin30°=m2gH
利用(1)中质量关系可求得m2下滑的最大距离H=
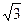 m="2.31" m
m="2.31" m
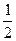 m1v12+
m1v12+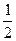 m22v2+m1g(A
m22v2+m1g(A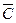 -A
-A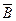 )sin30°=m2g·B
)sin30°=m2g·B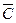
又由图示位置m1、m2受力平衡,应有:
Tcos∠ACB=m2g,T=m1gsin30°
又由速度分解知识知v1=v2cos∠ACB,代入数值可解得v2="2.15" m/s,
(2)m2下滑距离最大时m1、m2速度为零,在整个过程中应用机械能守恒定律,得:
ΔE增′=ΔE减′
即:m1g(
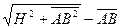 )sin30°=m2gH
)sin30°=m2gH利用(1)中质量关系可求得m2下滑的最大距离H=

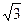 m="2.31" m
m="2.31" m
练习册系列答案
相关题目


 方向做加速运动(F和
方向做加速运动(F和 ,这个力的最小值是( )
,这个力的最小值是( )