题目内容
【题目】已知河宽L=300m，水速u=1m/s，船在静水中的速度v=3m/s，欲分别按下列要求过河时，船头应与河岸成多大角度？过河时间是多少？
（1）以最小位移过河；
（2）到达正对岸上游100m处．
【答案】（1）船头应指向上游河岸夹角的余弦值为
，过河位移最小为300m，所需要时间为106.1 s；
（2）要使船到达正对岸上游100m处，船头应与河岸成53°角度，过河时间是125 s．
【解析】分析：（1）当船航行方向与河岸方向垂直时，渡河位移最短，抓住等时性，结合垂直河岸方向的速度和河宽求出渡河的时间．
（2）将运动分解为垂直于河岸和平行于河岸进行分析，列出运动学方程即可求出渡河的时间及航向。
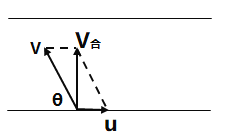
解：（1）船头应指向河岸上游，与河岸夹角为θ，有
解得： 
渡河时间为
≈106.1s
（2）设船头与上游河岸夹角为α，x=100m，则有
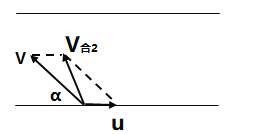
两式联立得 α=53°，t=125s
【题目】（1）在使用打点计时器来分析物体运动情况的实验中，有如下基本步骤：
A.把打点计时器固定在桌子上
B.安好纸带
C.松开纸带让物体带着纸带运动
D.接通低压交流电源
E.取下纸带
F.断开开关
这些步骤正确的排列顺序为____________________。
（2）用频率50Hz的打点计时器记录了被小车拖动的纸带的运动情况，在纸帶上确定出A、B、C、D、E、F、G共7个计数点，其相邻两点间的距离如图所示，每两个相邻的计数点之间还有4个点末画出。
①试根据纸带上各个计数点间的距离，计算出打下B、F两个点时小车的瞬时速度，并将各个速度值填人下表(要求保留三位有效数字，其中C、D、E三点已算出。)
|
|
|
|
| |
数值（m/s） | _______ | 0.479 | 0.560 | 0.640 | _______ |
②将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中，并画出小车的瞬时速度随时间变化的关系图线________。
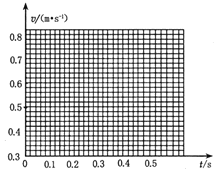
③由速度——时间图象求出小车的加速度为____________m/s2(该空保留两位有效数字)。
