题目内容
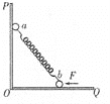
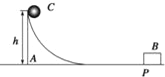
【题目】如图所示，一水平面上P点左侧光滑，右侧粗糙，质量为m的劈A在水平面上静止，上表面光滑，A右端与水平面平滑连接，质量为M的物块B恰好放在水平面上P点，物块B与水平面间的动摩擦因数为μ．一质量为m的小球C位于劈A的斜面上，距水平面的高度为h．小球C从静止开始滑下，然后与B发生正碰（碰撞时间极短，且无机械能损失）．已知M=2m，求：
①小球C与劈A分离时，A的速度；
②小球C的最后速度和物块B的运动时间．
【答案】①小球C与劈A分离时，A的速度为
；
②小球C的最后速度为
，方向向左，物块B的运动时间为 
．
【解析】分析：①小球下滑过程中，小球与劈A组成的系统在水平方向动量守恒，系统机械能守恒，由动量守恒定律与机械能守恒定律可以求出A与C分离时小球C的速度．
②小球C与物块B碰撞过程时间极短，碰撞过程动量守恒，由题意知B、C碰撞过程机械能守恒，由动量守恒定律与机械能守恒定律求出B与C的速度，碰后B做匀减速运动，由动量定理（或运动学公式）可以B的运动时间．
解：①设小球C与劈A分离时速度大小为v0，此时劈A速度大小为vA，小球C运动到劈A最低点的过程中，规定向右为正方向，系统水平方向动量守恒，机械能守恒，在水平方向，由动量守恒定律得： 
，
由机械能守恒定律得： 
，
解得： 
， 
，A的速度向左；
②小球C与B发生正碰后速度分别为vC和vB，碰撞过程动量守恒，规定向右为正方向，由动量守恒得： 
，
由机械能守恒定律得： 
，其中：M=2m，
解得： 
， 
，负号说明小球C最后向左运动，
物块B减速至停止时，运动时间设为t，由动量定理有
，
解得： 
。
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
