题目内容
6.某人站在高楼的平台边缘,以20m/s的初速度竖直向上抛出一石子,g=10m/s2,求(1)物体上升的最大高度是多少?回到抛出点的时间是多少?
(2)石子抛出后通过距抛出点下方20m处所需的时间.
分析 (1)物体做竖直上抛运动,应用匀变速运动的运动学公式可以求出高度与时间.
(2)应用匀变速直线运动的位移公式可以求出物体的运动时间.
解答 解:(1)物体做竖直上抛运动,
上升的最大高度:h=$\frac{{v}_{0}^{2}}{2g}$=$\frac{2{0}^{2}}{2×10}$=20m,
物体落回抛出点的时间:t=$\frac{2{v}_{0}}{g}$=$\frac{2×20}{10}$=4s;
(2)以向上为正方向,由题意可知:
v0=20m/s,a=-g=-10m/s2,x=-20m,
由匀变速直线运动的位移公式得:x=v0t+$\frac{1}{2}$at2,
即:-20=20t-$\frac{1}{2}$×10×t2,
解得:t=2(1+$\sqrt{2}$)s;
答:(1)物体上升的最大高度是20m,回到抛出点的时间是4s;
(2)石子抛出后落到距抛出点下方20m处所需的时间是2(1+$\sqrt{2}$)s.
点评 处理竖直上抛的运动的方法,可以分段运用运动学公式求解,也可以全过程运用运动学公式求解,知道竖直上抛运动上升过程和下降过程的对称性.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
16.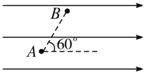 如图所示,A、B两点相距l=10cm,它们的连线与匀强电场场强方向夹角60°,把电子从A点移到B点,需克服电场力做功3.2×10-18J,则匀强电场的场强等于( )
如图所示,A、B两点相距l=10cm,它们的连线与匀强电场场强方向夹角60°,把电子从A点移到B点,需克服电场力做功3.2×10-18J,则匀强电场的场强等于( )
 如图所示,A、B两点相距l=10cm,它们的连线与匀强电场场强方向夹角60°,把电子从A点移到B点,需克服电场力做功3.2×10-18J,则匀强电场的场强等于( )
如图所示,A、B两点相距l=10cm,它们的连线与匀强电场场强方向夹角60°,把电子从A点移到B点,需克服电场力做功3.2×10-18J,则匀强电场的场强等于( )| A. | 800 N/C | B. | 400 N/C | C. | 400$\sqrt{3}$N/C | D. | 800$\sqrt{3}$N/C |
1.在如图所示的电路中,通过R1的电流I1是( )
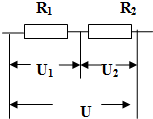

| A. | $\frac{U}{{R}_{1}}$ | B. | $\frac{{U}_{1}}{{R}_{1}}$ | C. | $\frac{{U}_{2}}{{R}_{2}}$ | D. | $\frac{U}{({R}_{1}+{R}_{2})}$ |
11.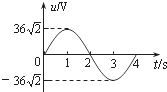 矩形线框在匀强磁场中绕垂直于磁场的轴匀速转动时,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
矩形线框在匀强磁场中绕垂直于磁场的轴匀速转动时,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
 矩形线框在匀强磁场中绕垂直于磁场的轴匀速转动时,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
矩形线框在匀强磁场中绕垂直于磁场的轴匀速转动时,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )| A. | 交流电压的有效值为36$\sqrt{2}$V | |
| B. | 交流电压的最大值为36$\sqrt{2}$V,频率为0.25Hz | |
| C. | 2s末线框平面垂直于磁场,通过线框的磁通量为零 | |
| D. | 1s末线框平面垂直于磁场,且电流的方向将改变 |
18. 如图甲所示,矩形导线框固定在匀强磁场中,磁感线的方向与导线框所在平面垂直,规定垂直纸面向里为磁场的正方向,磁感应强度B随时间t变化的规律如图乙所示,则( )
如图甲所示,矩形导线框固定在匀强磁场中,磁感线的方向与导线框所在平面垂直,规定垂直纸面向里为磁场的正方向,磁感应强度B随时间t变化的规律如图乙所示,则( )
 如图甲所示,矩形导线框固定在匀强磁场中,磁感线的方向与导线框所在平面垂直,规定垂直纸面向里为磁场的正方向,磁感应强度B随时间t变化的规律如图乙所示,则( )
如图甲所示,矩形导线框固定在匀强磁场中,磁感线的方向与导线框所在平面垂直,规定垂直纸面向里为磁场的正方向,磁感应强度B随时间t变化的规律如图乙所示,则( )| A. | 0到t1时间内,导线框中电流越来越小 | |
| B. | 0到t2时间内,导线框中电流的方向先为顺时针后为逆时针 | |
| C. | 0到t2时间内,导线框ab边受到的安培力越来越大 | |
| D. | 0到t2时间内,导线框有先扩张后收缩的趋势 |
15.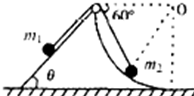 如图所示左侧是倾角θ=30°的斜面、右侧是圆弧面的物体固定在水平地面上,圆弧面底端切线水平,一根两端分别系有质量为m1,m2的小球的轻绳跨过其顶点上的小滑轮,当它们处于平衡状态时,连接m2的小球的轻绳与水平线的夹角为60°,不计一切摩擦,两小球可视为质点,两小球的质量之比等于( )
如图所示左侧是倾角θ=30°的斜面、右侧是圆弧面的物体固定在水平地面上,圆弧面底端切线水平,一根两端分别系有质量为m1,m2的小球的轻绳跨过其顶点上的小滑轮,当它们处于平衡状态时,连接m2的小球的轻绳与水平线的夹角为60°,不计一切摩擦,两小球可视为质点,两小球的质量之比等于( )
 如图所示左侧是倾角θ=30°的斜面、右侧是圆弧面的物体固定在水平地面上,圆弧面底端切线水平,一根两端分别系有质量为m1,m2的小球的轻绳跨过其顶点上的小滑轮,当它们处于平衡状态时,连接m2的小球的轻绳与水平线的夹角为60°,不计一切摩擦,两小球可视为质点,两小球的质量之比等于( )
如图所示左侧是倾角θ=30°的斜面、右侧是圆弧面的物体固定在水平地面上,圆弧面底端切线水平,一根两端分别系有质量为m1,m2的小球的轻绳跨过其顶点上的小滑轮,当它们处于平衡状态时,连接m2的小球的轻绳与水平线的夹角为60°,不计一切摩擦,两小球可视为质点,两小球的质量之比等于( )| A. | 2:$\sqrt{3}$ | B. | 2:3 | C. | $\sqrt{3}$:2 | D. | 1:1 |
16.关于分子势能,下列说法正确的是( )
| A. | 分子间表现为引力时,分子间距离越小,分子势能越大 | |
| B. | 分子间表现为斥力时,分子间距离越小,分子势能越大 | |
| C. | 物体在热胀冷缩时,分子势能发生变化 | |
| D. | 物体在做自由落体运动时,分子势能越来越小 |
 在平面直角坐标系xOy中,第Ⅰ象限存在匀强电场,第Ⅳ象限存在匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示.不计粒子重力,求
在平面直角坐标系xOy中,第Ⅰ象限存在匀强电场,第Ⅳ象限存在匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示.不计粒子重力,求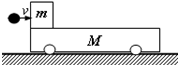 如图所示,在光滑水平面上静止着一辆质量为M=10kg的小车,车的上表面水平,小车左端有一质量为m=2kg的物块(可视为质点)处于静止状态,物块和车上表面之间的摩擦因数为μ=0.3,一质量为0.5kg的小球以10m/s的水平速度射向物块,碰撞后以2m/s的速度返回,木块不会从车上掉下来,求:
如图所示,在光滑水平面上静止着一辆质量为M=10kg的小车,车的上表面水平,小车左端有一质量为m=2kg的物块(可视为质点)处于静止状态,物块和车上表面之间的摩擦因数为μ=0.3,一质量为0.5kg的小球以10m/s的水平速度射向物块,碰撞后以2m/s的速度返回,木块不会从车上掉下来,求: