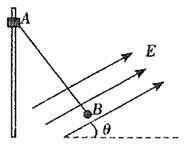
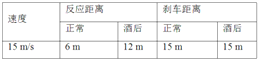
题目内容
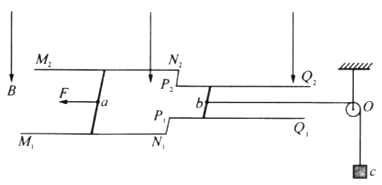
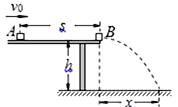
【题目】如图所示,质量为M的导体棒ab的电阻为r,水平放在相距为l的竖直光滑金属导轨上.导轨平面处于磁感应强度大小为B、方向垂直于导轨平面向外的匀强磁场中.左侧是水平放置、间距为d的平行金属板.导轨上方与一可变电阻R连接,导轨电阻不计,导体棒与导轨始终接触良好.重力加速度为g.
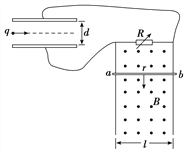
(1)调节可变电阻的阻值为R1=3r,释放导体棒,当棒沿导轨匀速下滑时,将带电量为+q的微粒沿金属板间的中心线水平射入金属板间,恰好能匀速通过.求棒下滑的速率v和带电微粒的质量m.
(2)改变可变电阻的阻值为R2=4r,同样在导体棒沿导轨匀速下滑时,将该微粒沿原来的中心线水平射入金属板间,若微粒最后碰到金属板并被吸收.求微粒在金属板间运动的时间t.
【答案】(1)![]() ,
,![]() (2)
(2)![]()
【解析】试题分析:棒匀速下滑,安培力与重力平衡,可求解棒下滑的速率。由于带电微粒在板间匀速运动,受力平衡可求带电微粒的质量;电压增大使微粒射入后向上偏转,由运动学规律可求微粒在金属板间运动的时间。
(1)棒匀速下滑,有![]()
回路中的电流![]()
将R1=3r代入棒下滑的速率![]()
金属板间的电压U=IR1
带电微粒在板间匀速运动,有![]()
联立解得带电微粒的质量![]()
(2)导体棒沿导轨匀速下滑,回路电流保持不变,金属板间的电压![]()
电压增大使微粒射入后向上偏转,有
![]() ,
,![]()
联立解得微粒在金属板间运动的时间![]()
【题型】解答题
【结束】
44
【题目】如图所示,光滑水平面上一质量为M、长为L的木板右端靠竖直墙壁.质量为m的小滑块(可视为质点)以水平速度v0滑上木板的左端,滑到木板的右端时速度恰好为零.

(1)求小滑块与木板间的摩擦力大小;
(2)现小滑块仍以水平速度v0从木板的右端向左滑动,求小滑块在木板上的滑行距离.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:对小物块进行分析,根据动能定理,小滑块与木板间的摩擦力大小;小滑块从右端向左滑动时,由动理守恒和能量守恒可求小滑块在木板上的滑行距离。
(1)对物块根据动能定理得
![]() 得
得![]()
(2)对滑块与木板组成的系统,设两者最后的共同速度为v1,
根据动量守恒定律得![]()
设小滑块相对木板滑行的距离为d,根据能量守恒定律得![]()
联立得![]()