题目内容
19.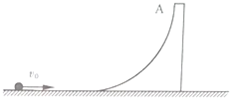 如图所示,质量M=2kg,半径R=0.3m的四分之一竖直光滑圆弧槽,静置在光滑水平面上,槽的末端和水平面相切,一质量m=1kg,可视为质点的光滑小球,以初速度v0冲上圆弧槽,g=10m/s2,求:
如图所示,质量M=2kg,半径R=0.3m的四分之一竖直光滑圆弧槽,静置在光滑水平面上,槽的末端和水平面相切,一质量m=1kg,可视为质点的光滑小球,以初速度v0冲上圆弧槽,g=10m/s2,求:(1)若槽固定在水平面上,要使小球恰好到达槽的最上端A点,v0应为多少
(2)若槽不固定,要使小球恰好到达槽的最上端A点,v0应为多少
(3)若槽不固定,当v0=6m/s时,圆弧槽最终获得的速度.
分析 (1)根据动能定理,抓住小球到达最高点的速度为零,求出初速度的大小.
(2)若槽不固定,小球到达最高点时与槽共速,在水平方向上动量守恒,结合动量守恒和机械能守恒求出初速度的大小.
(3)根据动量守恒和能量守恒求出圆弧槽最终获得的速度.
解答 解:(1)对小球,利用动能定理:-mgR=0-$\frac{1}{2}m{{v}_{0}}^{2}$.
得:${v}_{0}=\sqrt{2gR}=\sqrt{2×10×0.3}$m/s=$\sqrt{6}m/s$.
(2)小球恰好到达A点时,水平方向和槽共速,竖直方向速度为0.对系统,
规定小球的初速度方向为正方向,由动量守恒定律:mv0=(M+m)v,
由能量守恒定律:$mgR=\frac{1}{2}m{{v}_{0}}^{2}-\frac{1}{2}(m+M){v}^{2}$,
代入数据联立解得:v0=3m/s.
(3)当v0=6m/s时,小球到达A点时,水平方向仍和槽共速,故小球从A点离开槽后,还能再次从A点落回槽,并最终从槽的左侧离开槽.对系统:
规定小球的初速度方向为正方向,由动量守恒定律:mv0=mv1+Mv2,
由能量守恒定律:$\frac{1}{2}m{{v}_{0}}^{2}=\frac{1}{2}m{{v}_{1}}^{2}+\frac{1}{2}M{{v}_{2}}^{2}$,
代入数据解得:${v}_{2}=\frac{2m{v}_{0}}{m+M}=\frac{2×1×6}{1+2}=4m/s$,方向向右.
答:(1)v0应为$\sqrt{6}m/s$;
(2)v0应为3m/s.
(3)圆弧槽最终获得的速度为4m/s.
点评 本题考查了动量守恒和能量守恒的综合运用,综合性较强,对学生的能力要求较高,知道当槽不固定,小球恰好到达最高点时,两者具有共同的速度.

 53随堂测系列答案
53随堂测系列答案 如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,磁感强度为B的匀强磁场垂直穿过导轨平面.有一质量为m、长为l、电阻为R的导体棒,从ab位置以平行斜面的初速v向上运动,最远到达a′b′的位置,滑行的距离为s,与导轨之间的动摩擦因数为μ.则( )
如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,磁感强度为B的匀强磁场垂直穿过导轨平面.有一质量为m、长为l、电阻为R的导体棒,从ab位置以平行斜面的初速v向上运动,最远到达a′b′的位置,滑行的距离为s,与导轨之间的动摩擦因数为μ.则( )| A. | 上滑过程中导体棒受到的最大安培力为$\frac{{B}^{2}{l}^{2}v}{R}$ | |
| B. | 上滑过程中安培力、滑动摩擦力和重力对导体棒做的总功为$\frac{m{v}^{2}}{2}$ | |
| C. | 上滑过程中电流做功发出的热量为$\frac{m{v}^{2}}{2}$-mgs (sinθ+μcosθ) | |
| D. | 上滑过程中导体棒损失的机械能为$\frac{m{v}^{2}}{2}$-mgs sinθ |
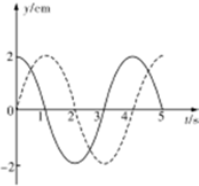
| A. | 波长一定是4cm | B. | 波的周期一定是4s | ||
| C. | 波的振幅一定是2cm | D. | 波的传播速度一定是1cm/s | ||
| E. | 波长可能是0.8cm |
| A. | 玛丽•居里首先提出原子的核式结构学说 | |
| B. | 卢瑟福在α粒子散射实验中发现了电子 | |
| C. | 查得威克在原子核人工转变的实验中发现了中子 | |
| D. | γ射线一般伴随着α或β射线产生,它的穿透能力最强 | |
| E. | γ射线在电场和磁场中都不会发生偏转 |
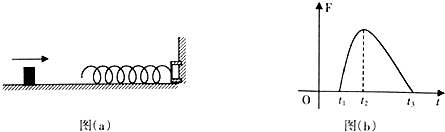
| A. | 小物块运动过程中不受摩擦力作用 | |
| B. | t2时刻小物块的动能最大 | |
| C. | t2-t3这段时间内,小物块的动能先增加后减少 | |
| D. | t2-t3这段时间内,小物块增加的动能等于弹簧减少的弹性势能 |
 如图所示,等边三角形ABC处在匀强电场中,其中电势φA=φB=0,电量为1C的正电荷仅在电场力作用下从C点运动到A点,电势能减少1J.保持该电场的大小和方向不变,让等边三角形以A点为轴在纸面内顺时针转过30°,则此时的B点电势为( )
如图所示,等边三角形ABC处在匀强电场中,其中电势φA=φB=0,电量为1C的正电荷仅在电场力作用下从C点运动到A点,电势能减少1J.保持该电场的大小和方向不变,让等边三角形以A点为轴在纸面内顺时针转过30°,则此时的B点电势为( )| A. | $\frac{\sqrt{3}}{3}$V | B. | $\frac{1}{2}$V | C. | -$\frac{\sqrt{3}}{3}$V | D. | -$\frac{1}{2}$V |
 如图1所示,是一个抽成真空的电子射线管,通电后管子左端的阴极能够发射电子.电子束从阴极向阳极运动,在通过图2示的磁场时将( )
如图1所示,是一个抽成真空的电子射线管,通电后管子左端的阴极能够发射电子.电子束从阴极向阳极运动,在通过图2示的磁场时将( )| A. | 向上偏转 | B. | 向下偏转 | C. | 向N极偏转 | D. | 向S极偏转 |
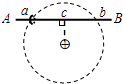 如图所示,光滑绝缘细杆AB水平置于被固定的带正电的可视为点电荷小球的正上方,小球的电荷量为Q.a、b是水平细杆上的两点,且在以带正电小球为圆心的同一竖直圆周上,c为a、b的中点.一个质量为m、电荷量为q的带负电的小圆环(可视为质点)套在细杆上,从a点由静止释放,在小圆环由a点运动到b点的过程中,下列说法中正确的是( )
如图所示,光滑绝缘细杆AB水平置于被固定的带正电的可视为点电荷小球的正上方,小球的电荷量为Q.a、b是水平细杆上的两点,且在以带正电小球为圆心的同一竖直圆周上,c为a、b的中点.一个质量为m、电荷量为q的带负电的小圆环(可视为质点)套在细杆上,从a点由静止释放,在小圆环由a点运动到b点的过程中,下列说法中正确的是( )| A. | 小圆环在c点的加速度最大 | |
| B. | 小圆环在b点的动能最大 | |
| C. | 小圆环与带电小球组成的系统的电势能在c点最大 | |
| D. | 小圆环与带电小球组成的系统的电势能在b两点最大 |
 由不同介质制成的两个半径均为R的透明四分之一圆柱体Ⅰ和Ⅱ紧靠在一起,截面如图所示,圆心为O,顶部交点为D,以O为原点建立直角坐标系xoy.红色光束1从介质Ⅰ底部的A(-$\frac{\sqrt{3}}{2}$R,0)点垂直于界面入射;红色光束2平行于y轴向下射入介质Ⅱ,入射点为B且∠BOD=60°.已知透明介质Ⅰ对红光的折射率n1=$\sqrt{2}$,透明介质Ⅱ对红光的折射率n2=$\sqrt{3}$.求:光束1经过柱面反射或折射后与y轴交点和光束2经柱体下底面折射后与y轴交点之间的距离.
由不同介质制成的两个半径均为R的透明四分之一圆柱体Ⅰ和Ⅱ紧靠在一起,截面如图所示,圆心为O,顶部交点为D,以O为原点建立直角坐标系xoy.红色光束1从介质Ⅰ底部的A(-$\frac{\sqrt{3}}{2}$R,0)点垂直于界面入射;红色光束2平行于y轴向下射入介质Ⅱ,入射点为B且∠BOD=60°.已知透明介质Ⅰ对红光的折射率n1=$\sqrt{2}$,透明介质Ⅱ对红光的折射率n2=$\sqrt{3}$.求:光束1经过柱面反射或折射后与y轴交点和光束2经柱体下底面折射后与y轴交点之间的距离.