题目内容
(14分)如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静时细线AB水平,细线AC与竖直方向的夹角θ=37º。已知小球的质量m=1kg,细线AC长L=1m,B点距C点的水平和竖直距离相等。(重力加速度g取10m/s2,sin37º=0.6,cos37º=0.8)
(1)若装置匀速转动的角速度为ω1时,细线AB上的张力为0而细线AC与竖直方向的夹角仍为37°,求角速度ω1的大小;
(2)若装置匀速转动的角速度为ω2时,细线AB刚好竖直,且张力为0,求此时角速度ω2的大小;
(3)装置可以以不同的角速度匀速转动,试通过计算在坐标图中画出细线AC上张力T随角速度的平方ω2变化的关系图像
(1)  rad/s (2)
rad/s (2)
(3)
解析试题分析:(1)细线AB上张力恰为零时有 (3分)
(3分)
解得 (1分)
(1分)
(2)细线AB恰好竖直,但张力为零时,由几何关系得 :
 (1分)
(1分)
此时 (3分)
(3分)
(3) 时,细线AB水平,细线AC上张力的竖直分量等于小球的重力
时,细线AB水平,细线AC上张力的竖直分量等于小球的重力

 (1分)
(1分) 时细线AB松弛
时细线AB松弛
细线AC上张力的水平分量等于小球做圆周运动需要的向心力
 (1分)
(1分) 时,细线AB在竖直方向绷直,仍然由细线AC上张力的水平分量提供小球做圆周运动需要的向心力
时,细线AB在竖直方向绷直,仍然由细线AC上张力的水平分量提供小球做圆周运动需要的向心力 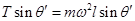
 (1分)
(1分)
综上所述  时,
时, 不变
不变 时,
时,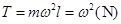 (1分)
(1分) 关系图象如图所示 (2分)
关系图象如图所示 (2分)
考点:圆周运动

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案2013年2月16日,在加拿大城市温哥华举行的第二十一届冬奥会花样滑冰双人自由滑比赛落下帷幕,中国选手申雪、赵宏博获得冠军.如右图所示,如果赵宏博以自己为转动轴拉着申雪做匀速圆周运动.若赵宏博的转速为30 r/min,手臂与竖直方向夹角为60°,申雪的质量是50 kg,她触地冰鞋的线速度为4.7 m/s,则下列说法正确的是( )
| A.申雪做圆周运动的角速度为2π rad/s |
| B.申雪触地冰鞋做圆周运动的半径约为2 m |
| C.赵宏博手臂拉力约是850 N |
| D.赵宏博手臂拉力约是500 N |
一艘小船在静水中的速度为4 m/s,渡过一条宽200 m,水流速度为5 m/s的河流,则该小船
| A.能到达正对岸 |
| B.以最短位移渡河时,位移大小为200m |
| C.渡河的时间可能少于50 s |
| D.以最短时间渡河时,沿水流方向的位移大小为250 m |
河水的流速与离河岸的关系如图甲所示,船在静水中速度与时间的关系如下图乙所示.若要使船以最短时间渡河,则( )
| A.船在行驶过程中,船头始终与河岸垂直 |
| B.船行驶的加速度大小始终为0.08m/s2 |
| C.船在河水中航行的轨迹是一条直线 |
| D.船在河水中的最大速度是5 m/s |



 ,则中轨道卫星的轨道处受地球引力产生的重力加速度约为 ( )
,则中轨道卫星的轨道处受地球引力产生的重力加速度约为 ( )
