��Ŀ����
����Ŀ����ͼ��A��C����ֱ�λ��x���y���ϣ� ![]() ��OC�ij���ΪL����
��OC�ij���ΪL����![]() �������д�ֱ��
�������д�ֱ��![]() ƽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB������Ϊm�������Ϊq�Ĵ��������ӣ�������ԭ������ų�������������
ƽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB������Ϊm�������Ϊq�Ĵ��������ӣ�������ԭ������ų�������������
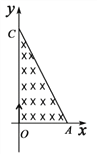
��1����������![]() ��������ų����������ڴų����˶����ʱ���Ƕ��٣���ʱ���ٶ�Ӧ����ʲô������
��������ų����������ڴų����˶����ʱ���Ƕ��٣���ʱ���ٶ�Ӧ����ʲô������
��2���������ٶȴ�СΪ![]() �������Բ�ͬ�ķ��������һ���ޣ����AC������������ڴų����˶������ʱ�䣬�������ӵ����䷽����X������ļнǡ�
�������Բ�ͬ�ķ��������һ���ޣ����AC������������ڴų����˶������ʱ�䣬�������ӵ����䷽����X������ļнǡ�
���𰸡���1��![]() ��2��
��2��![]() ��
�� ![]()
���������������������ת����Բ��OA�����ʱʱ��Ϊ��ֵ���ٶ�����������AC�����У����������˶��켣�����ݼ��ι�ϵ���뾶���������������ṩ�������������ٶȣ�Ҫʹ�����ڴų��о�����ʱ����̣���ʹ���ӹ켣��Ӧ���ҳ���̣����Թ�O������ֱ��CA���߶�Ϊ��̵��ң����ݼ��ι�ϵ���Բ�ĽǺ����ӵ����䷽����+x�ļнǣ�
��1������ת����Բ��OA�����ʱʱ��Ϊ��ֵ���ٶ�����������AC�����У���ͼ��ʾ��
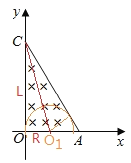
���ݼ��ι�ϵ�ɵã� ![]() ��
��
�������������ṩ�������ɵã� ![]() �����
�����![]() ��
��
�������������������ٶȷ�ΧΪ�� ![]() ��
��
�����ٶȴ�С��ȣ�Ҫʹ�����ڴų��о�����ʱ����̣���ʹ���ӹ켣��Ӧ���ҳ���̣��������ʱ��Ĺ켣��ͼ��ʾ��
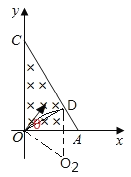
�����ڴų��е��˶��뾶Ϊ�� ![]() ���켣ͼ�м��ι�ϵ�ɵ�
���켣ͼ�м��ι�ϵ�ɵ�![]() ��
��
�ɴ˿�֪���ӹ켣��Ӧ��Բ�Ľ�Ϊ![]() �����ʱ��Ϊ��
�����ʱ��Ϊ�� ![]() ��
��
��ͼ��֪���������䷽����![]() ��ļн�Ϊ
��ļн�Ϊ![]() ��
��