题目内容
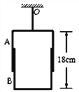
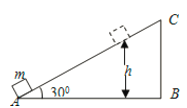
【题目】如图所示,一个质量为m的物体(可视为质点),由斜面底端的A点以某—初速度冲上倾角为30°的固定斜面做匀减速直线运动,减速的加速度大小为g,物体沿斜面上升的最大高度为h,在此过程中
A. 物体克服摩擦力做功![]() mgh
mgh
B. 物体的动能损失了mgh
C. 物体的重力势能增加了mgh
D. 系统机械能损失了mgh
【答案】CD
【解析】试题分析:设摩擦力大小为f.根据牛顿第二定律得:f+mgsin30°=ma,又a=g,解得 f=![]() mg,物体在斜面上能够上升的最大距离为2h,则物体克服摩擦力做功 Wf=f2h=mgh,故A错误.根据动能定理得:物体动能的变化量△Ek=W合=-ma2h=-2mgh,即动能损失了2mgh.故B错误.物体在斜面上能够上升的最大高度为h,所以重力势能增加了mgh,故C正确.根据功能原理可知,系统机械能减少量等于物体克服摩擦力做功Wf,为mgh,故D正确.故选CD。
mg,物体在斜面上能够上升的最大距离为2h,则物体克服摩擦力做功 Wf=f2h=mgh,故A错误.根据动能定理得:物体动能的变化量△Ek=W合=-ma2h=-2mgh,即动能损失了2mgh.故B错误.物体在斜面上能够上升的最大高度为h,所以重力势能增加了mgh,故C正确.根据功能原理可知,系统机械能减少量等于物体克服摩擦力做功Wf,为mgh,故D正确.故选CD。

练习册系列答案
相关题目