题目内容
【题目】如图所示为竖直平面内的两个半圆轨道，在B点平滑连接，两半圆的圆心O1、O2在同一水平线上，小半圆半径为R，大半圆半径为2R，一滑块从大的半圆一端A点以一定的初速度向上沿着半圆内壁运动，且刚好能通过大半圆的最高点，滑块从小半圆的左端向上运动，刚好能到达大半圆的最高点，大半圆内壁光滑，则（ ）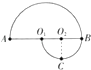
A.滑块在A的初速度为 
B.滑块在B点对小半圆的压力为6mg
C.滑块通过小半圆克服摩擦做的功力为mgR
D.增大滑块在A点的初速度，则滑块通过小半圆克服摩擦力做的功不变
【答案】B,C
【解析】解：A．由于滑块恰好能通过大的半圆的最高点，重力提供向心力，即mg=m 
，解得：v= 
，以AB面为参考面，根据机械能守恒定律可得： 
m 
=2mgR+ m（ ）2 ， 求得vA= 
，故A错误；
B．滑块在B点时对小圆轨道的压力为：F=m 
=6mg，故B正确；
C．设滑块在O1点的速度为v，则：v= 
=2 
，在小的半圆中运动过程中，根据动能定理Wf= m ﹣ mv2=mgR，故C正确；
D．增大滑块在A点的初速度，则物块在小的半圆中各个位置速度都增大，物块对半圆轨道的平均压力增大，因此克服摩擦力做的功增多，故D错误．
故选：BC．
滑块恰好能通过大的半圆的最高点，由重力提供向心力，即mg=m ，可求最高点的速度，再由机械能守恒定律可求滑块在A的初速度；
由牛顿第二定律可求滑块在B点对小半圆的压力；
根据动能定理求摩擦力做的功和分析正压力的变化情况，在讨论摩擦力做功的变化情况．
练习册系列答案
相关题目
