题目内容
如图所示，在xOy平面内的第一象限内存在沿Y轴正方向的匀强电场，在第四象限存在有界的磁场，磁感应强度B=9.0×10-3T，有一质量为m=9.0×10-31kg，电量为e=1.6×10-19C的电子以v0=2.0×107m/s的速度从Y轴的p点（0，2.5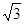
cm）沿X轴正方向射入第一象限，偏转后从X轴的Q点射入第四象限，方向与X轴成600角，在磁场中偏转后又回到Q点，方向与X轴也成600角。不计电子重力，求：
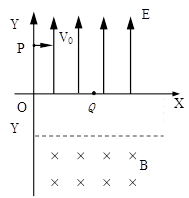
（1）OQ之间的距离及电子通过Q点的速度大小。
（2）若在第四象限内的磁场的边界为直线边界，即在虚线Y=Y0的下方有磁场，如图中所示。求Y0的坐标。
（3）若在第四象限内的磁场为圆形边界的磁场，圆形边界的磁场的圆心坐标的范围
（1）
v=
（2）、 
（3），- 
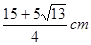≤y＜-5cm
解析:（1）电子在电场做类平抛运动，从P到Q过程中，
= ①
②
③
④
⑤
（2）电子在磁场中做匀速圆周运动
Bqv=m
⑥
由几何关系可知，电子回到Q点有：
⑦
⑧
（3）由几何关系可知，圆形磁场的圆心在Q点的正下方，即 ⑨
圆形磁场应与电子轨迹有公共弦，同时只要磁场半径r大于R即可
y=
⑩
圆形磁场在第四象限, 磁场半径应小于5cm, 由几何关系可知，
y= 
⑾
即圆形磁场的圆心的坐标应满足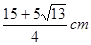： ，- ≤y＜-5cm
①3分②③④⑤各1分 ⑥⑦⑧各2分 ⑨1分⑩2分⑾2分
（2013?安徽模拟）如图所示，在xoy平面上，直线OM与x轴正方向夹角为45°，直线OM左侧存在平行y轴的匀强电场，方向沿y轴负方向．直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场．一带电量为q质量为m带正电的粒子（忽略重力）从原点O沿x轴正方向以速度vo射入磁场．此后，粒子穿过磁场与电场的边界三次，恰好从电场中回到原点O．（粒子通过边界时，其运动不受边界的影响）试求：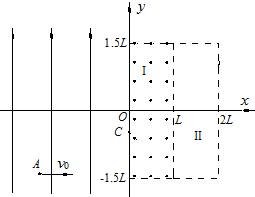
如图所示，在xOy平面的y轴左侧存在沿y轴正方向的匀强电场，y轴右侧区域Ⅰ内存在磁感应强度大小B1=
（2006?连云港二模）如图所示，在xoy平面上，一个以原点O为中心、半径为R的圆形区域内存在着一匀强磁场．磁场的磁感应强度为B，方向垂直于xoy平面向里．在O点处原来静止着一个具有放射性的原子核--氮（
如图所示，在xOy平面上，一个以原点O为圆心，半径为4R的原型磁场区域内存在着匀强磁场，磁场的方向垂直于纸面向里，在坐标（-2R，0）的A处静止着一个具有放射性的原子核氮713N．某时刻该核发生衰变，放出一个正电子和一个反冲核，已知正电子从A处射出时速度方向垂直于x轴，且后来通过了y轴，而反冲核刚好不离开磁场区域．不计重力影响和离子间的相互作用．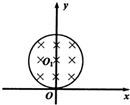
如图所示，在xOy平面上，以y轴上点Ol为圆心，半径为R=0.3m的圆形区域内，分布着一个方向垂直于xOy平面向里，磁感应强度大小为B=0.5T的匀强磁场．一个比荷