题目内容
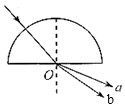
如图所示,一个厚度d=30
cm的军事设施,观察孔宽度L=60cm.为了扩大向外的观察视野,将折射率n=
的某种玻璃砖完全嵌入观察孔内(图中为观察孔的俯视图),则( )

| 3 |
| 3 |
| A.在观察孔的中央A处观察,视野角比安装前增大60° |
| B.在观察孔的中央A处观察,视野角比安装前增大90° |
| C.若观察者在孔的边缘E处观察,可以观察到在中央观察所看不到的位置 |
| D.要使在A处的视野角接近180°,则需嵌入折射率至少为n=2的玻璃砖 |

A、如图,由几何知识知折射角为30°,根据折射定律:
=
得sini=
i=60°
则视野角比安装前增大2(60°-30°)=60°
故A正确,B错误;
C、若观察者在孔的边缘E处观察,折射光线变为EO,则折射角变大,同样入射角变大,故可以观察到在中央观察所看不到的位置,C正确;
D、若要视野扩大到180°,即入射角为90°,而折射角r=30°不变,
则折射率n=
=2.故D正确;
故选:ACD.
| 3 |
| sini |
| sin30° |
得sini=
| ||
| 2 |
i=60°
则视野角比安装前增大2(60°-30°)=60°
故A正确,B错误;
C、若观察者在孔的边缘E处观察,折射光线变为EO,则折射角变大,同样入射角变大,故可以观察到在中央观察所看不到的位置,C正确;
D、若要视野扩大到180°,即入射角为90°,而折射角r=30°不变,
则折射率n=
| sin90° |
| sin30° |
故选:ACD.

练习册系列答案
相关题目
 ,液体中有一点光源S,上方空气中有一根很长的细杆,与液面的夹角为450,交点为A,且A点与点光源S的水平距离为0.1m,细杆与S在同一竖直平面内。要使点光源S所发生的光束照亮整个细杆,又不从A点左侧透射出水面,则点光源的深度h应满足什么条件?S所发出的光束与竖直方向的夹角在什么范围内?
,液体中有一点光源S,上方空气中有一根很长的细杆,与液面的夹角为450,交点为A,且A点与点光源S的水平距离为0.1m,细杆与S在同一竖直平面内。要使点光源S所发生的光束照亮整个细杆,又不从A点左侧透射出水面,则点光源的深度h应满足什么条件?S所发出的光束与竖直方向的夹角在什么范围内?