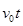题目内容
如图所示,水平地面的上空有一架飞机在进行投弹训练,飞机沿水平方向作匀加速直线运动.当飞机飞经观察点B点正上方A点时投放一颗炸弹,经时间T炸弹落在观察点B正前方L1处的C点,与此同时飞机投放出第二颗炸弹,最终落在距观察点B正前方L2处的D点,且L2=3L1,空气阻力不计.以下说法正确的有( )
| A.飞机第一次投弹的速度为L1/T |
| B.飞机第二次投弹时的速度为2L1/T |
| C.飞机水平飞行的加速度为L1/T2 |
| D.两次投弹时间间隔T内飞机飞行距离为4L1/3 |
AD
解析试题分析:(1)由题意可中第一次投弹时的水平位移,根据飞机的运动可知第二次投弹时飞机前进的距离,则由平抛运动的规律可求得两次投弹时飞机的速度;
(2)已知两次投弹时的速度,则由加速度的定义式可求得加速度的大小;
(3)根据匀加速运动位移速度公式即可求解两次投弹时间间隔T内飞机飞行距离.
A、第一次投放的炸弹水平位移:L1=V1T
第二次投放的炸弹水平位移为:S=V2T
飞机从第一次投弹到第二次投弹所发生的位移为:d= (V1+V2)T
(V1+V2)T
由几何关系可知:L2=d+S 由题意
有:L2=3L1
联立以上各式解得:V1=
V2=
故A正确,B错误;
C、设飞机沿水平方向作匀加速直线运动的加速度为a
由加速度公式可得:a=(V2﹣V1) =
= ,故C错误;
,故C错误;
D、根据匀加速运动位移速度公式得:
2ax=
解得:x= ,故D正确.
,故D正确.
故选AD
考点:平抛运动
点评:本题要特别注意飞机的运动,因飞机为匀变速运动,故两次抛出时的速度不同,但物体的速度与抛出时飞机的速度相同.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案由静止开始做匀加速直线运动的物体,在第1 s内的位移为2 m。关于该物体的运动情况,以下说法正确的是
| A.运动过程中的加速度为4 m/s2 |
| B.第1 s末的瞬时速度为2 m/s |
| C.第2 s内的位移为4 m |
| D.第1 s内的平均速度为4m/s |
摩托车以速度v1沿直线运动,突然驾驶员发现正前方s处,有一辆汽车正以v2(v2<v1)的速度开始减速,加速度大小为a2,为了避免发生碰撞,摩托车也同时减速,其加速度的最小值可能为( )
A. | B. |
C. | D. |
右图是伽利略1604年做斜面实验时的一页手稿照片,照片左上角的三列数据如下表。表中第二列是时间,第三列是物体沿斜面运动的距离,第一列是伽利略在分析实验数据时添加的。根据表中的数据.伽利略可以得出的结论是( )
| A.物体具有惯性 |
| B.斜面倾角一定时,加速度与质量无关 |
| C.物体运动的距离与时间的平方成正比 |
| D.物体运动的加速度与重力加速度成正比 |
如图所示,用一个沿斜面向上的恒力F将静止在斜面底端的物体加速向上推,推到斜面中点时,撤去恒力F,之后物体恰好运动到斜面顶端并返回。已知物体从底端运动到顶端所需时间以及从顶端滑到底端所需时间相等,物体回到底端时速度大小为10m/s,则( )
| A.恒力F与物体所受摩擦力之比为2:1 |
| B.物体所受重力与物体所受摩擦力之比为3:1 |
| C.撤去恒力F时物体的速度大小为10m/s |
| D.物体在沿斜面上升过程与下滑过程中加速度相等 |
某物体做直线运动,位移遵循的方程为x=6t-t2(其中,x的单位为m,t的单位为s)。则该物体在0~4s时间内通过的路程为( )
| A.8m | B.9m | C.10m | D.11m |
如图所示,在一直立的光滑管内放置一轻质弹簧,上端O点与管口A的距离为2xo,一质量为m的小球从管口由静止下落,将弹簧压缩至最低点B,压缩量为xo,不计空气阻力,则( ) 
| A.弹簧的最大弹性势能为3mgx。 |
B.小球运动的最大速度等于2 |
| C.弹簧的劲度系数为mg/x。 |
| D.小球运动中最大加速度为g |
质点做直线运动的位移x与时间t的关系为x=3t+t2(各物理量均采用国际制单位),则该质点
| A.该质点第2s内位移的大小是10m |
| B.任意1s内的速度增量都是2m/s |
| C.该质点的初速度为3m/s |
| D.任意相邻1s内的位移之差都是1m |