Question

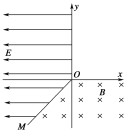
【题目】在xOy平面内，第Ⅲ象限内的直线OM是电场与磁场的边界，OM与x轴负方向成45°角．在x<0且OM的左侧空间存在着x轴负方向的匀强电场E，场强大小为32N/C，在y<0且OM的右侧空间存在着垂直纸面向里的匀强磁场B，磁感应强度大小为0.1T，如图所示．一不计重力的带负电的微粒，从坐标原点O沿y轴负方向以v0＝2×103m/s的初速度进入磁场，已知微粒的带电荷量为q＝5×10－18C，质量为m＝1×10－24kg。

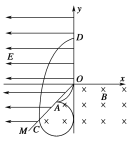
(1)画出带电微粒在磁场中运动的轨迹；

(2)求带电微粒第一次经过磁场边界时的位置坐标；

(3)求带电微粒最终离开电、磁场区域时的位置坐标；

(4)求带电微粒在电、磁场区域运动的总时间(结果保留三位有效数字)。

Answer 1

【答案】(1)见解析；(2)(－4×10－3m，－4×10－3m)；(3)(0，0.012)；(4)4.76×10－5s

【解析】

(1)带电微粒从O点射入磁场，在磁场中先经过圆周运动至A点，然后沿电场线方向进入匀强电场，向左做匀减速直线运动，然后第二次进入匀强磁场，经过圆周后，沿垂直于电场线的方向第二次进入匀强电场，其运动轨迹如图

(2)第一次经过磁场边界上的A点，由洛伦兹力公式和牛顿第二定律得

解得

r＝＝4×10－3m

A点位置坐标为(－4×10－3m，－4×10－3m)

(3)微粒从C点沿y轴正方向进入电场，做类平抛运动

解得

a＝1.60×108m/s2

解得

t1＝1×10－5s

Δy＝v0t1

代入数据解得

Δy＝0.02m

y＝Δy－2r＝(0.02－2×4×10－3)m＝1.2×10－2m

故离开电、磁场时的位置坐标为(0，0.012m)。

(4)带电微粒在磁场中运动的周期

在磁场中运动的时间

t2＝tOA＋tAC＝

代入数据解得

t2＝T＝1.26×10－5s

带电微粒第一次进入电场中做直线运动的时间

2.5×10－5s

带电微粒在电、磁场区域运动的总时间

t＝t1＋t2＋t3＝4.76×10－5s