题目内容
【题目】如图所示,在水平面内有一个正三角形边界和一个边长为l、每条边均为挡板的正六边形边界ABCDEF,在其六个顶点各开有一小孔,且正三角形边界与正六边形边界的几何中心重合.两边界之间的区域Ⅰ和六边形边界以内的区域Ⅱ均有垂直纸面向里的匀强磁场,三角形边界以外为真空.区域Ⅰ磁感应强度大小为4B0,区域Ⅱ磁感应强度大小为B0.现有大量质量均为m、电量均为q的正电粒子(粒子直径略小于小孔直径)从A点以大小不同的速度v垂直于AB边进入区域Ⅱ,若粒子与挡板撞击则速度立刻减为0,不计粒子的重力与粒子间的相互作用力,则:
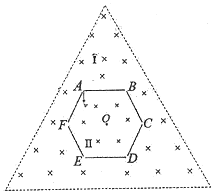
(1)求能从顶点C由区域Ⅱ射入区域Ⅰ的粒子速度的大小;
(2)求粒子最初从A点出发又回到A点经历的最短路程;
(3)为使所有粒子均不会从正三角形边界中飞出,求正三角形边界所围的最小面积.
【答案】(1) ![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)粒子能从C点由区域Ⅱ射入区域Ⅰ的粒子圆心在B点,轨迹半径R=l
又因为![]() ,所以
,所以![]() ;
;
(2)经分析,除一开始从发射点A运动到点D、并在点D由区域Ⅱ射入区域Ⅰ的粒子,其余粒子运动一段时间后均会与挡板相撞,速度减为0.
不与挡板相撞的粒子在区域Ⅱ运动轨迹的半径R1=2l,圆心角![]()
在区域Ⅰ磁感应强度变为4B0,运动轨迹的半径![]() ,圆心角
,圆心角![]()
可画出物理在两个磁场区域内的运动轨迹如图所示.
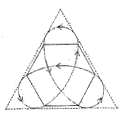
从A出发回到A的最短![]() ;
;
(3)如下图所示,画一个正三角形边界,使该三角形三条边均与区域Ⅰ中的三个半圆形轨迹相切.

由图可知,三角形![]()
边长![]()
![]()

练习册系列答案
相关题目