题目内容
【题目】如图所示,在倾角为θ的足够长的斜面上,有一个带风帆的滑板从静止开始沿斜面下滑,滑板的总质量为m,滑板与斜面间的动摩擦因数为μ,滑板上的风帆受到的空气阻力与滑板下滑的速度成正比,即f=kv.

(1)试求滑板下滑的最大速度vm的表达式;
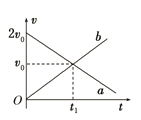
(2)若m=2 kg、θ=30°,g取10 m/s2,滑块从静止开始沿斜面下滑的速度—时间图象如图乙所示,图中斜线是t=0时刻的速度图象的切线.由此求μ和k的值.
【答案】(1)![]() (2)0.23,
(2)0.23,![]()
【解析】
(1)风帆受力如下图所示;
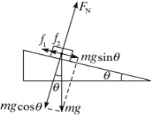
当mgsinθ=f1+f2时,风帆下滑的速度最大为vm
则有:mgsinθ=μmgcosθ+kvm
vm=![]() (sinθ-μcosθ).
(sinθ-μcosθ).
(2)由图象知t=0时风帆下滑的加速度:a=![]() m/s2=3 m/s2
m/s2=3 m/s2
风帆下滑过程中最大速度vm=2 m/s
当t=0时,由牛顿第二定律得:mgsinθ-μmgcosθ=ma
a=g(sinθ-μcosθ)=10×(0.5-![]() μ)=3 m/s2
μ)=3 m/s2
解得μ=0.23
由mgsinθ=mgμcoθ+kvm
得:k=![]() (sinθ-μcosθ)=
(sinθ-μcosθ)=![]() ×(0.5-0.23×
×(0.5-0.23×![]() )N/(m·s-1)=3 N/(m·s-1).
)N/(m·s-1)=3 N/(m·s-1).

练习册系列答案
相关题目