题目内容
18. 如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )
如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )| A. | 168cm | B. | 42cm | C. | 30cm | D. | 24cm |
分析 根据a、b两点状态状态,结合波形,确定ab间距离与波长的关系,求出波长的通项,再得到波长的特殊值.
解答 解:若波从a传到b,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则ab间距离为$\frac{3}{4}$λ或1$\frac{3}{4}$λ或2$\frac{3}{4}$λ…,得到通式xab=(k+$\frac{3}{4}$)λ(k=0,1,2…),由此可得到波长的可能值
λ=$\frac{{x}_{ab}}{k+\frac{3}{4}}=\frac{168}{4k+3}$cm
当k=0时,得到λ=56cm,此为波长最大值.
当k=1时,λ=24cm,
同理,若波从b传到a,则有xab=(k+$\frac{1}{4}$)λ(k=0,1,2…),由此可得到波长的可能值λ=$\frac{168}{4k+1}$cm
当k=0时,得到λ=168cm,此为波长最大值.
当k=1时,λ=33.6cm,
当k=2时,λ=18.7cm,
故AD正确.
故选:AD
点评 本题知道两个质点的状态,通过画出波形,确定出两点距离与波长的关系是常用的思路,注意要分两种情况讨论.

练习册系列答案
相关题目
9.下列说法正确的是( )
| A. | 放射性元素的半衰期是针对大量原子核的统计规律 | |
| B. | α、β、γ射线比较,α射线的电离作用最弱 | |
| C. | 光的波长越短,光子的能量越大,光的粒子性越明显 | |
| D. | 原子的全部正电荷和全部质量都集中在原子核里 |
6.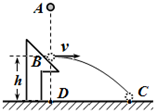 如图所示,从A点由静止释放一弹性小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同的时间落于地面上C点,已知地面上D点位于B点正下方,B、D间的距离为h,则( )
如图所示,从A点由静止释放一弹性小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同的时间落于地面上C点,已知地面上D点位于B点正下方,B、D间的距离为h,则( )
 如图所示,从A点由静止释放一弹性小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同的时间落于地面上C点,已知地面上D点位于B点正下方,B、D间的距离为h,则( )
如图所示,从A点由静止释放一弹性小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同的时间落于地面上C点,已知地面上D点位于B点正下方,B、D间的距离为h,则( )| A. | A、B两点间的距离为$\frac{h}{2}$ | B. | A、B两点间的距离为$\frac{h}{3}$ | ||
| C. | C、D两点间的距离为2h | D. | C、D两点间的距离为$\frac{2\sqrt{3}}{3}$h |
13.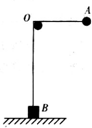 如图所示,一根长为L不可伸长的轻绳跨过光滑的水平轴O,两端分别连接质量均为m的小球A和物块B(A、B均视为质点),轻绳处于绷紧状态,由图示位置释放后,当小球A转动到水平轴正下方时轻绳的中点正好在水平轴O点,在此过程中,下列说法中正确的是( )
如图所示,一根长为L不可伸长的轻绳跨过光滑的水平轴O,两端分别连接质量均为m的小球A和物块B(A、B均视为质点),轻绳处于绷紧状态,由图示位置释放后,当小球A转动到水平轴正下方时轻绳的中点正好在水平轴O点,在此过程中,下列说法中正确的是( )
 如图所示,一根长为L不可伸长的轻绳跨过光滑的水平轴O,两端分别连接质量均为m的小球A和物块B(A、B均视为质点),轻绳处于绷紧状态,由图示位置释放后,当小球A转动到水平轴正下方时轻绳的中点正好在水平轴O点,在此过程中,下列说法中正确的是( )
如图所示,一根长为L不可伸长的轻绳跨过光滑的水平轴O,两端分别连接质量均为m的小球A和物块B(A、B均视为质点),轻绳处于绷紧状态,由图示位置释放后,当小球A转动到水平轴正下方时轻绳的中点正好在水平轴O点,在此过程中,下列说法中正确的是( )| A. | 物块B一直处于静止状态 | |
| B. | 小球A从图示位置运动到水平轴正下方的过程中机械能守恒 | |
| C. | 小球A运动到水平轴正下方时的速度等于$\sqrt{gL}$ | |
| D. | 小球A从图示位置运动到水平轴正下方的过程中,小球A与物块B组成的系统机械能守恒 |
3.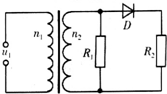 如图所示,理想变压器原、副线圈的匝数比n1:n2=11:5,原线圈接u1=110sin100πtV的交流电,电阻R1=R2=25Ω,D为理想二极管,则( )
如图所示,理想变压器原、副线圈的匝数比n1:n2=11:5,原线圈接u1=110sin100πtV的交流电,电阻R1=R2=25Ω,D为理想二极管,则( )
 如图所示,理想变压器原、副线圈的匝数比n1:n2=11:5,原线圈接u1=110sin100πtV的交流电,电阻R1=R2=25Ω,D为理想二极管,则( )
如图所示,理想变压器原、副线圈的匝数比n1:n2=11:5,原线圈接u1=110sin100πtV的交流电,电阻R1=R2=25Ω,D为理想二极管,则( )| A. | 通过电阻R1的电流为2A | B. | 二极管的反向耐压值应大于50V | ||
| C. | 原线圈的输入功率为200W | D. | 通过原线圈的电流为$\frac{15}{11}$A |
7.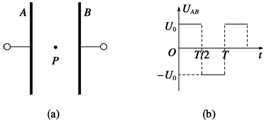 如图(a)所示,两平行正对的金属板A、B间加有如图(b)所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间P处.若在t0时刻释放该粒子,粒子会时而向A板运动,时而向B板运动,并最终打在A板上.则t0可能属于的时间段是( )
如图(a)所示,两平行正对的金属板A、B间加有如图(b)所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间P处.若在t0时刻释放该粒子,粒子会时而向A板运动,时而向B板运动,并最终打在A板上.则t0可能属于的时间段是( )
 如图(a)所示,两平行正对的金属板A、B间加有如图(b)所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间P处.若在t0时刻释放该粒子,粒子会时而向A板运动,时而向B板运动,并最终打在A板上.则t0可能属于的时间段是( )
如图(a)所示,两平行正对的金属板A、B间加有如图(b)所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间P处.若在t0时刻释放该粒子,粒子会时而向A板运动,时而向B板运动,并最终打在A板上.则t0可能属于的时间段是( )| A. | 0<t0<$\frac{T}{4}$ | B. | T<t0<$\frac{9T}{8}$ | C. | $\frac{3T}{4}$<t0<T | D. | $\frac{T}{2}$<t0<$\frac{3T}{4}$ |

 如图,水平轨道AB与竖直固定圆轨道相切于B点,C为圆轨道最高点,圆轨道半径R=5m.一质量m=60kg的志愿者,驾驶质量M=940kg、额定功率P=40kw的汽车体验通过圆轨道时所受底座的作用力,汽车从A点由静止以加速度a=2m/s2做匀加速运动,到达B点时,志愿者调节汽车牵引力,使汽车匀速率通过圆轨道又回到B点,志愿者在C点时所受底座的支持力等于志愿者的重力,已知汽车在水平轨道及圆轨道上的阻力均为汽车对轨道压力的0.1倍,取g=10m/s2,计算中将汽车视为质点.
如图,水平轨道AB与竖直固定圆轨道相切于B点,C为圆轨道最高点,圆轨道半径R=5m.一质量m=60kg的志愿者,驾驶质量M=940kg、额定功率P=40kw的汽车体验通过圆轨道时所受底座的作用力,汽车从A点由静止以加速度a=2m/s2做匀加速运动,到达B点时,志愿者调节汽车牵引力,使汽车匀速率通过圆轨道又回到B点,志愿者在C点时所受底座的支持力等于志愿者的重力,已知汽车在水平轨道及圆轨道上的阻力均为汽车对轨道压力的0.1倍,取g=10m/s2,计算中将汽车视为质点.