题目内容
7.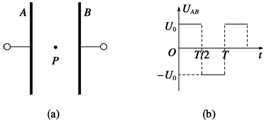 如图(a)所示,两平行正对的金属板A、B间加有如图(b)所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间P处.若在t0时刻释放该粒子,粒子会时而向A板运动,时而向B板运动,并最终打在A板上.则t0可能属于的时间段是( )
如图(a)所示,两平行正对的金属板A、B间加有如图(b)所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间P处.若在t0时刻释放该粒子,粒子会时而向A板运动,时而向B板运动,并最终打在A板上.则t0可能属于的时间段是( )| A. | 0<t0<$\frac{T}{4}$ | B. | T<t0<$\frac{9T}{8}$ | C. | $\frac{3T}{4}$<t0<T | D. | $\frac{T}{2}$<t0<$\frac{3T}{4}$ |
分析 解决此题首先要注意A、B两板电势的高低及带正电粒子运动的方向,再利用运动的对称性,粒子加速与减速交替进行运动,同时注意粒子向左、右运动位移的大小,即可判断各选项的对错.
解答 解:A、若$0<{t}_{0}<\frac{T}{4}$,带正电粒子先加速向B板运动、再减速运动至零;然后再反方向加速运动、减速运动至零;如此反复运动,每次向右运动的距离大于向左运动的距离,最终打在B板上,所以A错误.
B、若$T<{t}_{0}<\frac{9T}{8}$,带正电粒子先加速向B板运动、再减速运动至零;然后再反方向加速运动、减速运动至零;如此反复运动,每次向右运动的距离大于向左运动的距离,最终打在B板上,所以B错误.
C、若$\frac{3T}{4}<{t}_{0}<T$,带正电粒子先加速向A板运动、再减速运动至零;然后再反方向加速运动、减速运动至零;如此反复运动,每次向左运动的距离小于向右运动的距离,最终打在B板上,所以C错误.
D、若$\frac{T}{2}<{t}_{0}<\;\frac{3T}{4}$,带正电粒子先加速向A板运动、再减速运动至零;然后再反方向加速运动、减速运动至零;如此反复运动,每次向左运动的距离大于向右运动的距离,最终打在A板上,所以D正确.
故选:D.
点评 解决本题的关键会根据物体的受力判断物体的运动,通过加速度的方向与速度方向的关系得出物体的运动规律.本题也可以通过速度时间图象进行分析.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.奥斯特发现了电流的磁效应,由此揭开了电磁学的崭新时代的序幕,以下关于这段电磁学历史描述错误的是( )
| A. | 安培研究了电流间相互作用的规律,并提出了分子电流假说来解释磁现象 | |
| B. | 法拉第发现了电磁感应现象,并且给出了判断电磁感应电流大小和方向的定量规律 | |
| C. | 法拉第在研究电磁现象的过程中,提出了场的观点,认为电磁作用必须借助场作为媒介 | |
| D. | 麦克斯韦继承了法拉第关于场的观点,并进一步研究了电场和磁场的性质 |
18. 如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )
如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )
 如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )
如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )| A. | 168cm | B. | 42cm | C. | 30cm | D. | 24cm |
15. 如图所示,A、B分别为竖直放置的圆轨道的最低点和最高点,已知轨道半径为0.5m,小球通过A点时速度大小为2$\sqrt{7}$m/s,则该小球通过最高点B的速度值可能是( )
如图所示,A、B分别为竖直放置的圆轨道的最低点和最高点,已知轨道半径为0.5m,小球通过A点时速度大小为2$\sqrt{7}$m/s,则该小球通过最高点B的速度值可能是( )
 如图所示,A、B分别为竖直放置的圆轨道的最低点和最高点,已知轨道半径为0.5m,小球通过A点时速度大小为2$\sqrt{7}$m/s,则该小球通过最高点B的速度值可能是( )
如图所示,A、B分别为竖直放置的圆轨道的最低点和最高点,已知轨道半径为0.5m,小球通过A点时速度大小为2$\sqrt{7}$m/s,则该小球通过最高点B的速度值可能是( )| A. | 2.1m/s | B. | 3.2m/s | C. | 6.2m/s | D. | 10m/s |
12. 如图是简易测水平风速的装置,轻质塑料球用细线悬于竖直杆顶端O,当水平风吹来时,球在水平风力F的作用下飘起来.F与风速v成正比,当v=3m/s时,测得球平衡时细线与竖直方向的夹角θ=45°.则( )
如图是简易测水平风速的装置,轻质塑料球用细线悬于竖直杆顶端O,当水平风吹来时,球在水平风力F的作用下飘起来.F与风速v成正比,当v=3m/s时,测得球平衡时细线与竖直方向的夹角θ=45°.则( )
 如图是简易测水平风速的装置,轻质塑料球用细线悬于竖直杆顶端O,当水平风吹来时,球在水平风力F的作用下飘起来.F与风速v成正比,当v=3m/s时,测得球平衡时细线与竖直方向的夹角θ=45°.则( )
如图是简易测水平风速的装置,轻质塑料球用细线悬于竖直杆顶端O,当水平风吹来时,球在水平风力F的作用下飘起来.F与风速v成正比,当v=3m/s时,测得球平衡时细线与竖直方向的夹角θ=45°.则( )| A. | 当风速v=3m/s时,F的大小恰好等于球的重力 | |
| B. | 当风速v=6m/s时,θ=90° | |
| C. | 水平风力F越大,球平衡时,细线所受拉力越小 | |
| D. | 换用半径相等,但质量较小的球,则当θ=45°时,v大于3m/s |
19. 如图所示,当平行板电容器充电后,在极板间有一个用绝缘的细绳拴着带正电的小球,小球的质量为m,电荷量为q.现在向右偏θ角度;电源的电动势为ε,内阻为r.闭合电建S后,则求两极板间的距离d( )
如图所示,当平行板电容器充电后,在极板间有一个用绝缘的细绳拴着带正电的小球,小球的质量为m,电荷量为q.现在向右偏θ角度;电源的电动势为ε,内阻为r.闭合电建S后,则求两极板间的距离d( )
 如图所示,当平行板电容器充电后,在极板间有一个用绝缘的细绳拴着带正电的小球,小球的质量为m,电荷量为q.现在向右偏θ角度;电源的电动势为ε,内阻为r.闭合电建S后,则求两极板间的距离d( )
如图所示,当平行板电容器充电后,在极板间有一个用绝缘的细绳拴着带正电的小球,小球的质量为m,电荷量为q.现在向右偏θ角度;电源的电动势为ε,内阻为r.闭合电建S后,则求两极板间的距离d( )| A. | d=$\frac{εq}{mgtanθ}$ | B. | d=$\frac{εq}{mgsinθ}$ | C. | d=$\frac{mgtanθ}{E}$ | D. | d=$\frac{Eq}{mgsinθ}$ |
19. 如图所示,甲分子固定在坐标原点O,只在两分子间的作用力作用下,乙分子沿x轴方向运动,两分子间的分子势能Eρ与两分子间距离x的变化关系如图中曲线所示,设分子动能和势能之和为0,则( )
如图所示,甲分子固定在坐标原点O,只在两分子间的作用力作用下,乙分子沿x轴方向运动,两分子间的分子势能Eρ与两分子间距离x的变化关系如图中曲线所示,设分子动能和势能之和为0,则( )
 如图所示,甲分子固定在坐标原点O,只在两分子间的作用力作用下,乙分子沿x轴方向运动,两分子间的分子势能Eρ与两分子间距离x的变化关系如图中曲线所示,设分子动能和势能之和为0,则( )
如图所示,甲分子固定在坐标原点O,只在两分子间的作用力作用下,乙分子沿x轴方向运动,两分子间的分子势能Eρ与两分子间距离x的变化关系如图中曲线所示,设分子动能和势能之和为0,则( )| A. | 乙分子在P点(x=x2)时加速度最大 | B. | 乙分子在P点(x=x2)时动能最大 | ||
| C. | 乙分子在Q点(x=x1)时处于平衡状态 | D. | 乙分子在Q点(x=x1)时分子势能最小 |
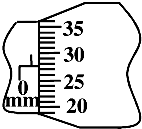 某同学利用双缝干涉实验装置测定某一光的波长,已知双缝间距为d,双缝到屏的距离为L,将测量头的分划板中心刻线与某一亮条纹的中心对齐,并将该条纹记为第一亮条纹,其示数如图所示,此时的示数x1=0.776mm.然后转动测量头,使分划板中心刻线与第n亮条纹的中心对齐,测出第n亮条纹示数为x2.由以上数据可求得该光的波长表达式λ=$\frac{d({x}_{2}-{x}_{1})}{L(n-1)}$(用给出的字母符号表示).
某同学利用双缝干涉实验装置测定某一光的波长,已知双缝间距为d,双缝到屏的距离为L,将测量头的分划板中心刻线与某一亮条纹的中心对齐,并将该条纹记为第一亮条纹,其示数如图所示,此时的示数x1=0.776mm.然后转动测量头,使分划板中心刻线与第n亮条纹的中心对齐,测出第n亮条纹示数为x2.由以上数据可求得该光的波长表达式λ=$\frac{d({x}_{2}-{x}_{1})}{L(n-1)}$(用给出的字母符号表示). 如图所示,固定的凹槽水平表面光滑,其内放置L形滑板P,滑板左端为半径R=1.0m的$\frac{1}{4}$圆弧面,A是圆弧的端点,BC段表面粗糙,长为L=3m,其余段表面光滑,小滑块P1和P2的质量均为m=1kg,滑板的质量M=4kg.P1和P2与BC面的动摩擦因数分别为μ1=0.10和μ2=0.40,最大静摩擦力近似等于滑动摩擦力,开始时滑板紧靠槽的左端,滑板的右端C与槽的右端相距x=0.1m,P2静止在粗糙面的B点,P1从A点正上方高为h=0.8m处自由落下,经过弧面与P2在B点发生弹性碰撞.滑板与槽的右端碰撞后与槽牢固粘连,P2与槽的碰撞为弹性碰撞,P1与P2视为质点,取g=10m/s2.求:
如图所示,固定的凹槽水平表面光滑,其内放置L形滑板P,滑板左端为半径R=1.0m的$\frac{1}{4}$圆弧面,A是圆弧的端点,BC段表面粗糙,长为L=3m,其余段表面光滑,小滑块P1和P2的质量均为m=1kg,滑板的质量M=4kg.P1和P2与BC面的动摩擦因数分别为μ1=0.10和μ2=0.40,最大静摩擦力近似等于滑动摩擦力,开始时滑板紧靠槽的左端,滑板的右端C与槽的右端相距x=0.1m,P2静止在粗糙面的B点,P1从A点正上方高为h=0.8m处自由落下,经过弧面与P2在B点发生弹性碰撞.滑板与槽的右端碰撞后与槽牢固粘连,P2与槽的碰撞为弹性碰撞,P1与P2视为质点,取g=10m/s2.求: