��Ŀ����
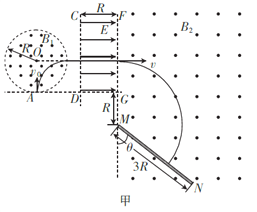
����Ŀ����ͼ��ʾ��Բ��ΪO���뾶ΪR��Բ������I���дŸ�Ӧǿ�ȴ�СΪB1������ֱֽ���������ǿ�ų����ų�����I�Ҳ���һ����ҲΪR���㹻���������������з������ҵ���ǿ�糡����������ұ߽�CD��FG��糡��ֱ������I�߽��Ϲ�A���������糡��ƽ������FG����G�㣬FG�Ҳ�Ϊ�������⡢�Ÿ�Ӧǿ�ȴ�СΪB2����ǿ�ų��������FG�ӳ����Ͼ�G��ΪR����M�����һ��Ϊ3R��ӫ����MN��ӫ������FG����=53��ǡ���A�㴦��һ������Դ������ֽ��������I�ڸ���������ȵط����������Ϊm���������Ϊ+q��������ͬ�����ӣ�������AO��������ų������ӣ�ǡ��ƽ���ڵ糡������������ֱ����ӫ�����ϣ���������������������ã�
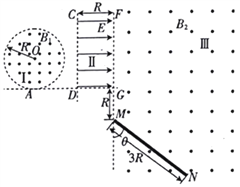
��1�������ӵij��ٶȴ�Сv0�͵糡�ĵ糡ǿ�ȴ�СE��
��2����ӫ�����ϵķ���������x��
��3�����ı�������дų��ĴŸ�Ӧǿ�ȴ�С��Ҫ����������ȫ������ӫ��������������дų��ĴŸ�Ӧǿ�ȴ�СӦ�����������
���𰸡���1��![]() ;
; ![]() (2)
(2) ![]() (3)
(3) ![]()
����������1)��ͼ����ʾ��������֪������������I�е��˶��뾶ΪR����������
��ʽ�ɵ�![]() �����
�����![]()
�����Ӵ�ֱ����ӫ�����ϣ��������֪����������е��˶��뾶Ϊ2R������������ʽ�ɵ�![]() �����
�����![]()
�����ڵ糡�м����˶����ɶ��ܶ�����![]()
��õ糡ǿ�ȴ�С![]()
��2����ͼ����ʾ��

������֪���ٶȷ�����糡����ƽ��������������I�е����ӽ�ƽ�е糡���������I����ߵ㴩����������M��x1�������ϣ��ɼ��ι�ϵ��![]()
���![]()
�ٶȷ�����糡����ƽ��������������I�е����ӽ�ƽ�е糡���������I����͵㴩����������M��![]() �������ϣ��ɼ��ι�ϵ��
�������ϣ��ɼ��ι�ϵ��![]()
���![]()
������֪�������Ӿ�δƽ����FG������ڰ��ϣ����ӫ�����ϵķ�������![]() ��
��
��3����ͼ����ʾ��

������I����ߵ㴩��������ǡ�ô���M��ʱ����![]()
����������ʽ��![]() �����
�����![]()
������ƽ����FG�������N��ʱ���ɼ��ι�ϵ��![]()
�����������е���������M��![]() ����Ȼ���Ӳ�����ƽ����FG�������N��
����Ȼ���Ӳ�����ƽ����FG�������N��
����G�������������N��������˶��뾶Ϊ��������뾶���ɼ��ι�ϵ��![]()
��![]() ����������ʽ��
����������ʽ��![]() �����
�����![]()
Ҫ����������ȫ������ӫ������������еĴŸ�Ӧǿ�ȴ�СӦ���ǵ������ǣ� ![]()