题目内容
【题目】某一长直的赛道上，有一辆F1赛车前方200 m处有一安全车正以10 m/s的速度匀速前进，这时赛车从静止出发以2 m/s2的加速度追赶。试求：
(1)追上之前与安全车最远相距是多少米？
(2)赛车何时追上安全车？
(3)当赛车刚追上安全车时，赛车手立即刹车，使赛车以4 m/s2的加速度做匀减速直线运动，问两车再经过多长时间第二次相遇？（设赛车可以从安全车旁经过而不发生相撞）
【答案】(1)225m(2)20s（3）20s
【解析】试题分析：当速度相等时，两车相距最远，结合速度时间公式求出速度相等经历的时间，根据位移关系求出相距的最大距离；根据位移关系，结合运动学公式求出追及的时间；根据位移关系，结合运动学公式求出第二次相遇的时间，注意赛车速度减为零后不再运动。
（1）当赛车的速度与安全车的速度相等时，相距最远，
速度相等经历的时间为： 
此时赛车位移： 
安全车位移为： 
两车距离
可得： 
，故两车相距的最远距离为225m
（2）设赛车经过时间t1追上安全车，
根据位移关系有： 
代入数据解得：t1=20s
（3）第一次相遇时赛车的速度
设第一次相遇起再经过时间t2再次相遇，则
解得：t2=15s
但赛车速度从40m/s减为零只需10s
可知赛车速度减为零时，安全车还未追上赛车，根据位移关系有： 
解得：t3=20s
故经过20s再次相遇
科学实验活动册系列答案
【题目】某实验小组用如图所示的装置测自由落体的加速度，其操作步骤如下：
A．按照图中的装置安装实验器材 |
B．将打点计时器接到学生电源的“直流输出”上 |
C．先释放纸带，之后闭合开关接通电源，打出一条纸带 |
D．重复步骤C几次，从打出的纸带中选取较理想的一条测量并研究 |
E．根据测量的数据算出重力加速度
（1）以上步骤中有错误请指出其错误步骤（填代号）并改正： ；
（2）利用图像可以求出重力加速度，乙物体下落速度的二次方
为纵轴，以下落的高度h为横轴，做出图线为一条直线，若图线的斜率为k，则重力加速度
。
（3）若实验中所得到的重物下落的加速度值小于当地的重力加速度值，而实验操作与数据处理均无错误，写出一个你认为可能引起此误差的原因： 。
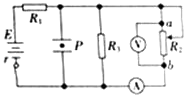
【题目】在测量电源的电动势和内阻的实验中，由于所用的电压表（视为理想电压表）的量程较小，某同学设计了如图所示的实物电路．
（1）实验时，应先将电阻箱的电阻调到 ． （选填“最大值”、“最小值”或“任意值”）
（2）改变电阻箱的阻值R，分别测出阻值R0=10Ω的定值电阻两端的电压U，下列两组R的取值方案中，比较合理的方案是 ． （选填“1”或“2”）
方案编号 | 电阻箱的阻值R/Ω | ||||
1 | 400.0 | 350.0 | 300.0 | 250.0 | 200.0 |
2 | 80.0 | 70.0 | 60.0 | 50.0 | 40.0 |
（3）根据实验数据描点，绘出的 
图象是一条直线．若直线的斜率为k，在 
坐标轴上的截距为b，则该电源的电动势E= ， 内阻r= ． （用k、b和R0表示）
