Question

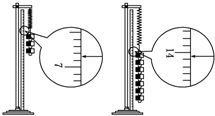
（2009?威海模拟）如图所示，光滑坡道顶端距水平面高度为h，质量为m的小物块A从坡道顶端由静止滑下，进入水平面上的滑道，经过O点时无机械能损失，为使A制动，将轻弹簧的一端固定在竖直墙上的M点，另一端恰位于滑道的末端O点．已知在OM段，物块A与水平面间的动摩擦因数均为μ，其余各处的摩擦不计，重力加速度为g，求：
（1）物块滑到O点时的速度大小；
（2）弹簧为最大压缩量d时的弹性势能（设弹簧处于原长时弹性势能为零）；
（3）若物块A能够被弹回到坡道上，则它能够上升的最大高度是多少？

Answer 1

分析：（1）物块从A运动到O的过程中，重力做功mgh，根据动能定理求出物块滑到O点时的速度大小．
（2）物块从在水平轨道上运动时，克服摩擦力做功，物块的动能转化为弹簧的弹性势能和内能，根据能量守恒定律求出弹簧为最大压缩量d时的弹性势能．
（3）物块A被弹回的过程中，克服摩擦力和重力做功，再由能量守恒定律求解物块能够上升的最大高度．

解答：解：
（1）设物块A到达O点的速度大小为v，由动能定理：
     mgh=

1

2

mv2-0
     解得：v=

2gh

（2）物块A在水平滑道上克服摩擦力做功为W=μmgd
由能量守恒定律得：

1

2

mv2=Ep+W
解得：E_p=mgh-μmgd
（3）物块A被弹回的过程中，克服摩擦力做功仍为W
由能量守恒定律得：Ep=W+mgh/
解得：h′=h-2μd
答：（1）物块滑到O点时的速度大小为

2gh

；
（2）弹簧为最大压缩量d时的弹性势能为mgh-μmgd；
（3）若物块A能够被弹回到坡道上，则它能够上升的最大高度是h-2μd．

点评：本题涉及三个过程，关键要确定出能量如何转化，根据能量守恒定律列方程．