题目内容
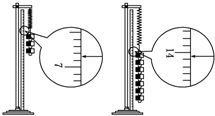
（2009?威海模拟）一条不可伸长的轻绳跨过质量可忽略不计的定滑轮，绳的一端系一质量M=15kg的重物，重物静止于地面上，有一质量m=10kg的猴从绳子另一端沿绳向上爬，如图所示，不计滑轮摩擦，在重物不离开地面条件下，猴子向上爬的最大加速度为（g=10m/s2）（ ）分析：当小猴以最大加速度向上爬行时，重物对地压力为零，故小猴对细绳的拉力等于重物的重力，对小猴受力分析，运用牛顿第二定律求解加速度．
解答：解：小猴以最大加速度向上爬行时，重物对地压力为零，故小猴对细绳的拉力等于重物的重力，即F=Mg；
小猴对细绳的拉力等于细绳对小猴的拉力F′=F；
对小猴受力分析，受重力和拉力，根据牛顿第二定律，有
F′-mg=ma
解得
a=
=5m/s2
故选B．
小猴对细绳的拉力等于细绳对小猴的拉力F′=F；
对小猴受力分析，受重力和拉力，根据牛顿第二定律，有
F′-mg=ma
解得
a=
| (M-m)g |
| m |
故选B．
点评：本题关键先后对重物和小猴受力分析，然后根据共点力平衡条件和牛顿第二定律列式求解．
练习册系列答案
天天向上口算本系列答案
相关题目
（2009?威海模拟）在我国乒乓球运动有广泛的群众基础，并有“国球”的美誉，在2008年北京奥运会上中国选手包揽了四个项目的全部冠军．现讨论乒乓球发球问题，已知球台长L、网高h，若球在球台边缘O点正上方某高度处，以一定的垂直球网的水平速度发出，如图所示，球恰好在最高点时刚好越过球网．假设乒乓球反弹前后水平分速度不变，竖直分速度大小不变、方向相反，且不考虑乒乓球的旋转和空气阻力．则根据以上信息可以求出（设重力加速度为g）（ ）