题目内容
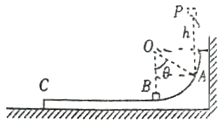
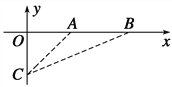
【题目】如图所示,固定在水平面上的光滑斜面OA与水平面间的夹角为a=37°,轻弹簧下端固定在0点,上可自由伸长到A点。在A点放一个可视为质点的物块,对物块施加一沿斜面的力F,使物块缓慢向下缩弹簧至C点(弹簧一直处在弹性限度内),该过程中力F随弹簧压缩长度x的变化情况如图2所示。已知重力加速度g取10 m/s2,sin 370=0.6,cos 37°=0.8,则下列说法正确的是( )

A. 物块的质量为15 kg
B. 弹簧从A点被压缩到C点的过程中,力F所做的功为180 J
C. 弹簧在C点时具有的弹性势能为105J
D. 在C点撤去外力F后.物块返回到A点时的速度为5m/s
【答案】C
【解析】
当x=0时弹簧的弹力为零,通过列出平衡方程求解m;F-x图像的“面积”等于力F的功;根据能量关系分析弹簧在C点的弹性势能;回到A点时的动能等于力F的功,求解回到A点时的速度.
由图像可知当x=0时,F=30N,即mgsin370=F=30,解得m=5kg,选项A错误;由F-x图像可知,弹簧从A点被压缩到C点的过程中,力F所做的功为![]() ,选项B错误;由能量关系可知,弹簧在C点时具有的弹性势能为
,选项B错误;由能量关系可知,弹簧在C点时具有的弹性势能为![]() ,选项C正确;因力F做功90J,则撤去F后,回到A点时的动能为90J,即
,选项C正确;因力F做功90J,则撤去F后,回到A点时的动能为90J,即![]() ,则va=6m/s
,则va=6m/s
即物块返回到A点时的速度为6m/s,选项D错误;故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目