题目内容
【题目】如图所示，地面固定一个圆心为O、竖直放置的光滑半圆轨道ABC，B为半圆轨道中点，半径R=0.08m，∠COB=90°.木板DE 质量为m，长度L=10m，E与A距离S=2m，木板与地面间的动摩擦因数为μ1=0.1，木板与A碰撞后立即原速率返回，并由地面控制装置（图中末画出）保证E与A只能碰撞一次。E与A等高，以使E与A重合时板上的物体可以滑入半圆轨道，当E与A一旦分离，板上物块将落地而无 法进入半圆轨道。一个可看作质点的物体质量为2m，物体与木板间动摩擦因数为μ2=0.2，物体在合适的位 置以合适的初速度v0开始向右运动，重力加速度g=10m/s2，结果可保留根号。求：
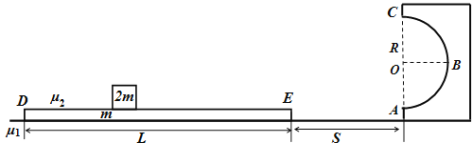
(1)要使物体沿轨道刚能到达 B 点，物体在 A 处的速度 vA 的大小；
(2)要使物体能到达 C 点而不脱离轨道，物体初速度v0 的取值范围.
【答案】（1）
（2）6m/s≤v0≤8m/s
【解析】
(1)对物体，从A到B： -mgR=
-
刚能到达B处时：vB=0
解得:
(2)设物体在A点的速度为v1，从A到C：-mg2R =
要使物体能到达C点不脱离轨道，在C处有：mg=
解得:v1=2m/s
根据分析，可分为如下两种情形进行求解：
情形①：当物体相对木板从左端的D点滑到E时，木板恰好运动了S=2m使E与A相遇，而且物体速度大于v1时，物体对应的v0有最大值
设木板加速度大小为，物体的加速度大小为a2
对木板有：μ2·2mg-μ1·3mg=ma1
可得：a1=1m/s2
对物体有:μ22mg=2ma2
可得：a2=2m/s2
设木板运动到与A相碰所用时间为t1，则板和物体的位移关系有：
L=
解得: t1=2s，v0=8m/s
此时物体到A的速度：v=v0-a2t1=4m/s
故v0=8m/s是v0的最大值
情形②：当物体与木板达到共速时物体恰好滑到E，以后一起减速运动直到E与A相遇，而且物体速度等于v1时，物体对应的v0有最小值
设物体与木板一起运动的加速度大小为a3，有：μ13mg=3ma3
求得：a3= 1m/s2
设物体与木板达到共速
所用时间为t2，板在t2时间内位移为S2，两者一起运动的位移为S3，则=
又板的总位移： 
解得：t2=2s，v0= 6m/s
故初速度的取值范围为：6m/s≤v0≤8m/s
