题目内容
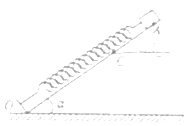
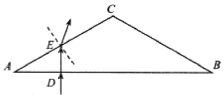
【题目】如图所示，实线为一条光滑的金属轨道，其中
为完整圆轨道，在水平地面接触处交错分开，B为部分圆轨道，不同几何形状的轨道之间均平滑连接.一可视为质点的小球从水平地面上轨道的C点以满足条件的初速度向左运动，经过B的外侧轨道，再经过A的内侧轨道运动到D点，小球始终没有脱离轨道.已知B圆轨道的半径为R，则（ ）
A. 小球在
点速度
应该满足：
B. 小球在C点速度应该满足：
C. A圆轨道半径
应该满足：
D. A圆轨道半径应该满足：
【答案】AD
【解析】
AB. 要使小球能够到达B点且不脱离，在B点的最小速度为零，对应小球在
点的速度最小，根据机械能守恒：
，
；
在B点的最大向心力为mg，此时速度为
，对应小球在点的速度最大，根据机械能守恒：
，
；故小球在点速度
应该满足：
，故A正确，B错误；
CD. 设A轨道半径为r，要使小球在A圆轨道不脱离轨道，在A圆轨道最高点的最小速度为
，对应小球在C点的速度最小，根据机械能守恒：
，
，所以A圆轨道半径
应该满足：
，故C错误，D正确。
故选：AD
练习册系列答案
阅读快车系列答案
相关题目
