题目内容
【题目】如图所示，一滑板放置在光滑的水平地面上，右侧紧贴竖直墙壁，滑板由圆心为O、半径为R的四分之一光滑圆弧轨道和水平轨道两部分组成，且两轨道在B点平滑连接，整个系统处于同一竖直平面内。现有一可视为质点的小物块从A点正上方P点处由静止释放，落到A点的瞬间垂直于轨道方向的分速度立即变为零，之后沿圆弧轨道AB继续下滑，最终小物块恰好滑至轨道末端C点处。已知滑板的质量是小物块质量的3倍，小物块滑至B点时对轨道的压力为其重力的3倍，OA与竖直方向的夹角为θ=60°，小物块与水平轨道间的动摩擦因数为μ=0.3，重力加速度g取10
，不考虑空气阻力作用，求：
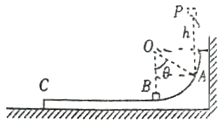
（1）水平轨道BC的长度L；
（2）P点到A点的距离h。
【答案】（1）2.5R（2）
R
【解析】
（1）物块从A到B的过程中滑板静止不动，先根据物块在B点的受力情况求解B点的速度；滑块向左滑动时，滑板向左也滑动，根据动量守恒和能量关系列式可求解水平部分的长度；（2）从P到A列出能量关系；在A点沿轨道切向方向和垂直轨道方向分解速度；根据机械能守恒列出从A到B的方程；联立求解h。
（1）在B点时，由牛顿第二定律：
，其中NB=3mg；
解得
；
从B点向C点滑动的过程中，系统的动量守恒，则
；
由能量关系可知：
联立解得：L=2.5R；
（2）从P到A点，由机械能守恒：mgh=
mvA2；
在A点：
，
从A点到B点：
联立解得h=R
练习册系列答案
相关题目
