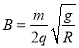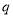题目内容
如图所示，倾角分别为37°和53°的两足够长绝缘斜面上端以光滑小圆弧平滑对接，左侧斜面光滑，斜面某处存在着矩形匀强磁场区域MNQP，磁场方向垂直于斜面向上，MN平行于斜面底边，
。ab与PQ相距0.5m。一不可伸长的绝缘细轻绳跨过斜面顶端，一端连接着可视为质点的带正电薄板，一端连接在单匝正方形金属线框abcd的ab边中点，ab //MN，细绳平行于斜面侧边，线框与薄板均静止在斜面上，ab与PQ相距0.5m。已知薄板电荷量q=1×10–4 C，薄板与线框的质量均为m=0.5kg，薄板与右侧斜面间的动摩擦因数μ=0.3，线框电阻R=1Ω，线框边长0.5m。（g=10 m/s2，sin37°=0.6，斜面固定，不计绳与斜面的摩擦）
（1）求薄板静止时受到的摩擦力。
（2）现在右侧斜面上方加一场强大小E= 9×103 N/C，方向沿斜面向下的匀强电场，使薄板沿斜面向下运动，线框恰能做匀速运动通过磁场；在线框的cd边刚好离开磁场时，将电场方向即刻变为垂直于右侧斜面向下（场强大小不变），线框与薄板做减速运动最后停在各自的斜面上。求磁感应强度大小B和cd边最终与MN的距离x。
（1）1 N 沿右侧斜面向上 （2）x=2. 94 m
【解析】
试题分析：(1)设绳的张力大小为T，薄板所受静摩擦力大小为f
对线框由平衡条件有
(2分)
对薄板由平衡条件有
(2分)
联立以上两式代入数据解得f=1 N (1分)
摩擦力方向沿右侧斜面向上 (1分)
(2)设线框边长为L，线框做匀速运动时的速率为v，在磁场中受到的安培力为F，电场方向改变前后薄板受到的摩擦力大小分别为f1和f2
在ab进入磁场前的过程中: 
由能量守恒定律有
(2分)
代入数据解得v=1 m/s (1分)
线框在磁场中做匀速运动时:
(1分)
对线框由平衡条件有
(1分)
对薄板由平衡条件有
(1分)
联立以上三式代入数据解得B=2 T (1分)
在cd穿出磁场后的过程中:
(1分)
因为
，
所以绳子不会松弛，将和线框一起做减速运动
由能量守恒定律有
(2分)
代入数据解得
考点：本题考查物体平衡条件、能量守恒定律和安培力。
