Question

(12分)如图所示，在倾角θ＝37°的光滑斜面上存在一垂直斜面向上的匀强磁场区域MNPQ，磁感应强度B的大小为5T，磁场宽度d＝0.55m，有一边长L＝0.4m、质量m1＝0.6kg、电阻R＝2Ω的正方形均匀导体线框abcd通过一轻质细线跨过光滑的定滑轮与一质量为m2＝0.4kg的物体相连，物体与水平面间的动摩擦因数μ＝0.4，将线框从图示位置由静止释放，物体到定滑轮的距离足够长．(取g＝10m/s2，sin37°＝0.6，cos37°＝0.8)求：

(1)线框abcd还未进入磁场的运动过程中，细线中的拉力为多少？

(2)当ab边刚进入磁场时，线框恰好做匀速直线运动，求线框刚释放时ab边距磁场MN边界的距离x多大？（3）在（2）问的条件下，若cd边恰好离开磁场边界PQ时，速度大小为2m/s，求整个过程中ab边产生的热量为多少？

 

Answer 1

(1)2.4 N　(2)0.25 m　(3)0.1 J

【解析】

试题分析：(1)m1、m2运动过程中，以整体法有

m1gsin θ－μm2g＝(m1＋m2)a

a＝2 m/s2

以m2为研究对象有T－μm2g＝m2a(或以m1为研究对象有m1gsin θ－T＝m1a

T＝2.4 N

(2)线框进入磁场恰好做匀速直线运动，以整体法有

m1gsin θ－μm2g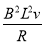－＝0

v＝1 m/s

ab到MN前线框做匀加速运动，有

v2＝2axx＝0.25 m

(3)线框从开始运动到cd边恰离开磁场边界PQ时：

m1gsin θ(x＋d＋L)－μm2g(x＋d＋L)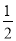＝ (m1＋m2)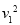＋Q

解得：Q＝0.4 J

所以Qab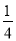＝Q＝0.1 J

考点：牛顿第二定律及能量守恒定律；