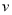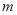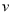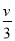题目内容
如图所示，在水平绝缘轨道的末端N处，平滑连接一个半径为R的光滑绝缘的半圆形轨道，整个空间存在一个场强大小
，方向水平向左的匀强电场，并在半圆轨道区域内还存在一个垂直纸面向里的匀强磁场，磁感应强度
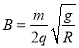。现在有一个带正电的小物块(可看作质点)，质量为m，电量为
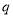，从距N点
的地方静止释放。已知物块与水平轨道之间的动摩擦因数
，重力加速度取g，求：
（1）小物块运动到轨道的最高点P时，小物块对轨道的压力；
（2）小物块从P点离开半圆轨道后，又落在水平轨道距N点多远的地方。
(1) 物块对轨道的压力为4mg，方向竖直向上 (2)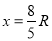 
【解析】
试题分析：（1）小物块从水平轨道上释放后一直到P点，由动能定理可得：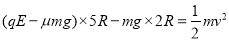
（3分）
解得：
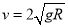(1分)
在P点，由受力分析，可得：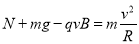
（3分）
可得：
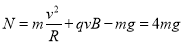（1分）
由牛顿第三定律，小物块对轨道的压力为4mg，方向竖直向上； (1分)
（2）小物块离开轨道后，水平方向做加速度向左的匀减速直线运动，竖直方向做自由落体运动，根据分位移公式，有：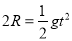
（2分）
（2分）
根据牛顿第二定律有：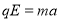
（2分）
解得：
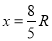（2分）
考点：本题考查了匀电势差和电场强度的关系、带电粒子在匀强磁场中的运动、牛顿运动定律．
练习册系列答案
阅读快车系列答案
相关题目
