题目内容
如图,水平地面上方有一底部带有小孔的绝缘弹性竖直挡板,板高h=9m,与板上端等高处水平线上有一P点,P点离挡板的距离S=3m.板的左侧以及板上端与P点的连线上方存在匀强磁场和匀强电场.磁场方向垂直纸面向里,磁感应强度B=1T;比荷大小 可视为质点的小球从挡板下端处小孔以不同的速度水平射入场中做匀速圆周运动,若与挡板相碰就以原速率弹回,且碰撞时间不计,碰撞时电量不变,小球最后都能经过位置P,g=10m/s2,求:
可视为质点的小球从挡板下端处小孔以不同的速度水平射入场中做匀速圆周运动,若与挡板相碰就以原速率弹回,且碰撞时间不计,碰撞时电量不变,小球最后都能经过位置P,g=10m/s2,求:

(1)电场强度的大小与方向;
(2)小球不与挡板相碰运动到P的时间;
(3)要使小球运动到P点时间最长应以多大的速度射入.
10V/m,竖直向下 π+arcsin (s) 3.75m/s
(s) 3.75m/s
【解析】
试题分析:(1)因小球做匀速圆周运动,有:Eq=mg得:E= =10V/m,方向竖直向下;
=10V/m,方向竖直向下;
(2)小球不与挡板相碰直接到达P点轨迹如图:
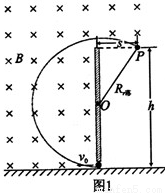
有:(h-R)2+s2=R2 得:R=5m PO与挡板夹角为θ,则sinθ=
小球圆周运动周期T=
设小球圆周运动圆弧的圆心角为α,则t=
运动时间t= =π+arcsin
=π+arcsin (s);
(s);
(3)因速度方向与半径垂直,原先必在挡板线上,
设小球与挡板碰撞n次,有R≤ 又R≥s n只能取0,1.n=0即(2)问不符合题意
又R≥s n只能取0,1.n=0即(2)问不符合题意
n=1时有(h-3R)2+s2=R2
解得:R1=3m,R2=3.75m
轨迹如图,半径为R2时运动时间最长

洛伦兹力提供向心力:qvB= 得:v=3.75m/s
得:v=3.75m/s
考点:本题考查带电粒子在匀强磁场中的运动;带电粒子在匀强电场中的运动.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目









