题目内容
16.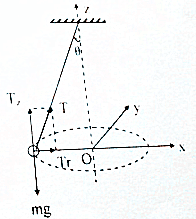 有一锥面摆,物体的质量为m,物体在水平面内以匀速率v作圆周运动,圆周半径为R,摆线与竖直方向的夹角为θ,求运行一周过程中,
有一锥面摆,物体的质量为m,物体在水平面内以匀速率v作圆周运动,圆周半径为R,摆线与竖直方向的夹角为θ,求运行一周过程中,(1)物体所受重力mg的冲量Ig;
(2)摆线对物体的拉力T的冲量$\overline{{I}_{T}}$;
(3)物体所受合力的冲量$\overline{I}$.
分析 根据线速度和周期的关系求出周期.再由冲量的定义可求得重力的冲量;由动量定理可求得拉力的冲量.
解答  解:(1)周期为:T=$\frac{2πR}{v}$;设向下为正方向;
解:(1)周期为:T=$\frac{2πR}{v}$;设向下为正方向;
一个周期内重力的冲量Ig=mgT=$\frac{2mgπR}{v}$;方向竖直向下;
(2)在转动一周的过程中,物体的动量变化为零;故合外力的冲量为零;
则由动量定理可知,细绳拉力的冲量等于重力的冲量;
故$\overline{{I}_{T}}$=-Ig=-$\frac{2mgπR}{v}$;负号说明拉力的冲量与重力的冲量方向相反,即竖直向上;
答:(1)物体所受重力mg的冲量Ig为$\frac{2mgπR}{v}$;方向竖直向下;
(2)摆线对物体的拉力T的冲量$\overline{{I}_{T}}$为$\frac{2mgπR}{v}$;方向竖直向下;
(3)物体所受合力的冲量$\overline{I}$为0.
点评 本题考查动量定理的应用,由于动量、冲量均为矢量,在解题时要注意明确动量的矢量性.

练习册系列答案
相关题目
6.物体做自由落体运动,下落时间为总时间的一半时,动能为EK1,下落距离为高度的一半时,动能为EK2,那么EK1和EK2的大小关系是( )
| A. | EK1>EK2 | B. | EK1<EK2 | C. | EK1=EK2 | D. | 无法确定 |
7.下列关于人造地球卫星与宇宙飞船的说法中,正确的是( )
| A. | 如果知道地球公转的轨道半径和周期,再利用万有引力常量,就可以算出地球的质量 | |
| B. | 如果知道人造地球卫星的轨道半径和它的周期,再利用万有引力常量,就可以算出地球的质量 | |
| C. | 两颗人造地球卫星,只要它们的绕行速率相等,不管它们的质量、形状差别有多大,它们的绕行半径和绕行周期都一定是相同的 | |
| D. | 原来在同一轨道上沿同一方向绕行的人造卫星一前一后,若要使后一卫星追上前一卫星并实现对接,只要将后者的速率增大一些即可 |
8.关于电源,下列说法正确的是( )
| A. | 电源是将电能转化为其他形式的能的装置 | |
| B. | 电源是把电子从正极经电源内部搬运到负极的装置 | |
| C. | 电源的作用是使导线中形成静电场 | |
| D. | 电源的作用是维持导线两端一定的电势差 |
4.甲、乙两质点间的万有引力大小为F,若甲物体的质量不变,乙物体的质量增加到原来的2倍,同时它们之间的距离减为原来的$\frac{1}{2}$,则甲、乙物体的万有引力大小将变为( )
| A. | $\frac{F}{8}$ | B. | 4F | C. | 8F | D. | 12F |
 物体从斜角为θ高为h的斜面顶端自静止开始滑下,又在水平面上滑行了一段距离而停止.已知停下来后物体离斜面底端距离为S,如图所示,物体与斜面及物体与水平面间的动摩擦因数相同,斜面末端与水平面由光滑弧面连接,求物体与斜面(或与水平面)间的动摩擦因数μ.
物体从斜角为θ高为h的斜面顶端自静止开始滑下,又在水平面上滑行了一段距离而停止.已知停下来后物体离斜面底端距离为S,如图所示,物体与斜面及物体与水平面间的动摩擦因数相同,斜面末端与水平面由光滑弧面连接,求物体与斜面(或与水平面)间的动摩擦因数μ.