��Ŀ����
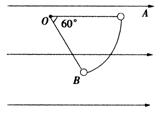
��ͼ��ʾ���ó�Ϊl�ľ�Եϸ��˩һ������Ϊm��������Ϊ+q��С����Ϊ�ʵ㣩��������O�㣬����װ�ô���ˮƽ���ҵ���ǿ�糡�У���С������ʹ���߳�ˮƽ��λ��A���ɾ�ֹ��ʼ��С���ͷţ�С���A�㿪ʼ���°ڶ���������ת��![]() �ǵ���λ��Bʱ���ٶ�ǡ��Ϊ�㣮��
�ǵ���λ��Bʱ���ٶ�ǡ��Ϊ�㣮��
��1��B��A����ĵ��Ʋ�UBA��
��2���糡ǿ��E��
��3��С��B��ʱ�����߶�С�������T��
��4��С���A�˶���B������е�����ٶ�vm�����߶�С����������Tm��
��1�����ݶ��ܶ�����mglsin![]() �C qUBA = 0 , B��A����ĵ��Ʋ�UBA =
�C qUBA = 0 , B��A����ĵ��Ʋ�UBA =![]() (2��)
(2��)
��2���糡ǿ��E =![]() (2��)
(2��)
��3��С��B��ʱ�����������ͼ��ʾ�����߶�С�������T�������ذ뾶����ķ���mgcos![]() ���糡���ذ뾶����ķ���qEcos
���糡���ذ뾶����ķ���qEcos![]() �ĺ���������������ΪvB = 0
�ĺ���������������ΪvB = 0
T �Cmgcos![]() �CqEcos
�CqEcos![]() = 0 ���T =
= 0 ���T =![]() (2��)
(2��)
��4��С���A��B������дﵽ����ٶ�vmʱ��С�����ܺ����ķ����ذ뾶���������߷���ĺ���Ϊ�㣮���ʱ������ˮƽ����ļн�Ϊ![]() ����С�����������ش�ֱ�뾶����ķ���mgcos
����С�����������ش�ֱ�뾶����ķ���mgcos![]() ��糡���ش�ֱ�뾶����ķ���qEsin
��糡���ش�ֱ�뾶����ķ���qEsin![]() ��ȣ�
��ȣ�
��mgcos![]() = qEsin
= qEsin![]() ��tan
��tan![]() =
=![]() ��
��![]() =
=![]() (2��)
(2��)
�ɶ��ܶ�����mglsin![]() �C Eql (1 �C cos
�C Eql (1 �C cos![]() ) =
) =![]() ��
��
�ɽ��vm =![]() =
=![]() (2��)
(2��)

���߶�С�������Tm�������ذ뾶����ķ���mgsin![]() ���糡���ذ뾶����ķ��� qE cos
���糡���ذ뾶����ķ��� qE cos![]() �ĺ�������������Tm �C mgsin
�������������Tm �C mgsin![]() �C qEcos
�C qEcos![]() = m
= m![]() �� ���Tm = (6 �C 2
�� ���Tm = (6 �C 2![]() ) mg�� (2��)
) mg�� (2��)
����:
��

 ��ͼ��ʾ���ó�ΪL��ϸ��˩������Ϊm��С������ֱƽ������Բ���˶���������˵������ȷ���ǣ�������
��ͼ��ʾ���ó�ΪL��ϸ��˩������Ϊm��С������ֱƽ������Բ���˶���������˵������ȷ���ǣ�������A����С��պ�������ֱƽ������Բ���˶���������ߵ������Ϊ
| ||
| B��С������ߵ�ʱ���ӵ�����������Ϊ�� | ||
| C��С����Բ����ߵ�ʱ���ܵ�������һ��Ϊ���� | ||
| D��С�����͵�ʱ���ӵ�����һ��С��С������ |
 ��ͼ��ʾ���ó�ΪL����������һ����Ϊm��С��С����ʩ��һ������ʹ������ֱ����ɦ½Dz�������С���ھ�ֹ״̬��������СֵΪ
��ͼ��ʾ���ó�ΪL����������һ����Ϊm��С��С����ʩ��һ������ʹ������ֱ����ɦ½Dz�������С���ھ�ֹ״̬��������СֵΪ ��2003?�麣ģ�⣩��ͼ��ʾ���ó�ΪL����������һ������Ϊm��С��С����ʩ��һ������ʹ������ֱ����ɦ½Dz�������С���ھ�ֹ״̬��������СΪ��������
��2003?�麣ģ�⣩��ͼ��ʾ���ó�ΪL����������һ������Ϊm��С��С����ʩ��һ������ʹ������ֱ����ɦ½Dz�������С���ھ�ֹ״̬��������СΪ�������� ��ͼ��ʾ���ó�ΪL��ϸ������һ������Ϊm��С������ΪO�㣬��С������A�㣬ʹ������ˮƽ�����30��ǣ�Ȼ�����֣��ʣ�С���˶�����������·�B��ʱ�������е�����Ϊ���
��ͼ��ʾ���ó�ΪL��ϸ������һ������Ϊm��С������ΪO�㣬��С������A�㣬ʹ������ˮƽ�����30��ǣ�Ȼ�����֣��ʣ�С���˶�����������·�B��ʱ�������е�����Ϊ��� ��2012?��ƽ����ģ����ͼ��ʾ���ó�ΪL�ľ�Եϸ������һ����С��С�������Ϊm�������Ϊq���ּ�һˮƽ�������ǿ�糡��ƽ��ʱС��ֹ��M�㣬ϸ������ֱ����ɦȽǣ�
��2012?��ƽ����ģ����ͼ��ʾ���ó�ΪL�ľ�Եϸ������һ����С��С�������Ϊm�������Ϊq���ּ�һˮƽ�������ǿ�糡��ƽ��ʱС��ֹ��M�㣬ϸ������ֱ����ɦȽǣ�