题目内容
 如图所示,用长为L的细绳悬挂一个质量为m的小球,悬点为O点,把小球拉至A点,使悬线与水平方向成30°角,然后松手,问:小球运动到悬点的正下方B点时,悬线中的张力为多大?
如图所示,用长为L的细绳悬挂一个质量为m的小球,悬点为O点,把小球拉至A点,使悬线与水平方向成30°角,然后松手,问:小球运动到悬点的正下方B点时,悬线中的张力为多大?分析:小球先做自由落体运动,由机械能守恒可求得绳子绷紧时的速度,但要注意绳子绷紧的瞬间小球的径向分速度消失,由速度的合成与分解求出切向分量;此后的过程中机械能守恒,可求得小球到达B点的速度,由向心力公式可求得悬线中的张力.
解答: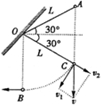 解:在A点松手后,绳子为松弛状态,所以小球在重力作用下做自由落体运动,当小球落到A点的正下方C点,OC=L时绳又被拉紧,此时由于绳子的冲量作用,使小球沿绳方向的速度分量υ2减小为0,小球将以L为半径、υ1为初速度从C开始做圆周运动,如图.因此,从A点到B点的过程中有机械能损失,机械能不守恒.当小球从C点运动到B点的过程中,机械能守恒.本题应先求出小球在C点时的切向速度υ1,再对CB段运用机械能守恒定律求出υ,最后求绳中张力T.
解:在A点松手后,绳子为松弛状态,所以小球在重力作用下做自由落体运动,当小球落到A点的正下方C点,OC=L时绳又被拉紧,此时由于绳子的冲量作用,使小球沿绳方向的速度分量υ2减小为0,小球将以L为半径、υ1为初速度从C开始做圆周运动,如图.因此,从A点到B点的过程中有机械能损失,机械能不守恒.当小球从C点运动到B点的过程中,机械能守恒.本题应先求出小球在C点时的切向速度υ1,再对CB段运用机械能守恒定律求出υ,最后求绳中张力T.
小球从A点到C点做自由落体运动,下落高度为L,则:υC=
.
其切向分量为:υ1=υCcos30°=
小球从C点到B点过程中,由机械能守恒定律有:
mgL(1-sin30°)=
m
-
m
将υ1代入解得:υB2=
gL
对B点由向心力公式得:T-mg=m
解得:T=mg+m
=
mg.
答:悬线中的张力为
.
 解:在A点松手后,绳子为松弛状态,所以小球在重力作用下做自由落体运动,当小球落到A点的正下方C点,OC=L时绳又被拉紧,此时由于绳子的冲量作用,使小球沿绳方向的速度分量υ2减小为0,小球将以L为半径、υ1为初速度从C开始做圆周运动,如图.因此,从A点到B点的过程中有机械能损失,机械能不守恒.当小球从C点运动到B点的过程中,机械能守恒.本题应先求出小球在C点时的切向速度υ1,再对CB段运用机械能守恒定律求出υ,最后求绳中张力T.
解:在A点松手后,绳子为松弛状态,所以小球在重力作用下做自由落体运动,当小球落到A点的正下方C点,OC=L时绳又被拉紧,此时由于绳子的冲量作用,使小球沿绳方向的速度分量υ2减小为0,小球将以L为半径、υ1为初速度从C开始做圆周运动,如图.因此,从A点到B点的过程中有机械能损失,机械能不守恒.当小球从C点运动到B点的过程中,机械能守恒.本题应先求出小球在C点时的切向速度υ1,再对CB段运用机械能守恒定律求出υ,最后求绳中张力T.小球从A点到C点做自由落体运动,下落高度为L,则:υC=
| 2gL |
其切向分量为:υ1=υCcos30°=
| ||
| 2 |
小球从C点到B点过程中,由机械能守恒定律有:
mgL(1-sin30°)=
| 1 |
| 2 |
| υ | 2 B |
| 1 |
| 2 |
| υ | 2 1 |
将υ1代入解得:υB2=
| 5 |
| 2 |
对B点由向心力公式得:T-mg=m
| ||
| L |
解得:T=mg+m
| ||
| L |
| 7 |
| 2 |
答:悬线中的张力为
| 7mg |
| 2 |
点评:本题考查机械能的守恒定律应用与向心力公式的结合,难点在于绳子绷紧时的分析,要知道绳子不能形变,导致瞬间速度发生了变化,只保留了切向分速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做圆周运动,则下列说法中正确的是( )
如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做圆周运动,则下列说法中正确的是( )A、若小球刚好能在竖直平面内做圆周运动,则在最高点的速率为
| ||
| B、小球在最高点时绳子的拉力不可能为零 | ||
| C、小球在圆周最高点时所受的向心力一定为重力 | ||
| D、小球过最低点时绳子的拉力一定小于小球重力 |
 如图所示,用长为L的轻绳悬挂一质量为m的小球,对小球再施加一个力,使绳与竖直方向成β角并绷紧,小球处于静止状态,此力最小值为
如图所示,用长为L的轻绳悬挂一质量为m的小球,对小球再施加一个力,使绳与竖直方向成β角并绷紧,小球处于静止状态,此力最小值为 (2003?珠海模拟)如图所示,用长为L的轻绳悬挂一个质量为m的小球,对小球再施加一个力,使绳与竖直方向成β角并绷紧,小球处于静止状态,此力最小为( )
(2003?珠海模拟)如图所示,用长为L的轻绳悬挂一个质量为m的小球,对小球再施加一个力,使绳与竖直方向成β角并绷紧,小球处于静止状态,此力最小为( ) (2012?昌平区二模)如图所示,用长为L的绝缘细线悬挂一带电小球,小球的质量为m、电荷量为q.现加一水平向左的匀强电场,平衡时小球静止于M点,细线与竖直方向成θ角.
(2012?昌平区二模)如图所示,用长为L的绝缘细线悬挂一带电小球,小球的质量为m、电荷量为q.现加一水平向左的匀强电场,平衡时小球静止于M点,细线与竖直方向成θ角.