题目内容
如图所示，用长为L的轻绳悬挂一质量为m的小球，对小球再施加一个力，使绳与竖直方向成β角并绷紧，小球处于静止状态，此力最小值为mgsinβ
mgsinβ
．分析：以小球为研究对象，分析受力情况：重力mg，绳的拉力T和力F，根据平衡条件的推论可知，绳的拉力T和力F的合力大小等于mg，方向竖直向上，保持不变，根据作图法，确定力F最小时F的方向，再根据平衡条件求出F的最小值．
解答：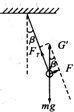
解：以小球为研究对象，则小球受重力mg，绳拉力FT，施加外力F，应有F与FT合力与mg等大反向，即F与FT的合力为G′=mg．如图所示，
在合力G′一定时，其一分力FT方向一定的前提下，另一分力的最小值由三角形定则可知F应垂直绳所在的直线，故F=mgsinβ．
故答案为：mgsinβ．
解：以小球为研究对象，则小球受重力mg，绳拉力FT，施加外力F，应有F与FT合力与mg等大反向，即F与FT的合力为G′=mg．如图所示，在合力G′一定时，其一分力FT方向一定的前提下，另一分力的最小值由三角形定则可知F应垂直绳所在的直线，故F=mgsinβ．
故答案为：mgsinβ．
点评：用力的矢量三角形定则分析力的极值问题的实质是数形结合求极值的一种方法．数形结合在数学中是常用的一种方法．实质上，所有矢量都可以利用这种数形结合的形式求极值．
练习册系列答案
相关题目
（2003?珠海模拟）如图所示，用长为L的轻绳悬挂一个质量为m的小球，对小球再施加一个力，使绳与竖直方向成β角并绷紧，小球处于静止状态，此力最小为（ ）
如图所示，用长为L的细绳悬挂一个质量为m的小球，悬点为O点，把小球拉至A点，使悬线与水平方向成30°角，然后松手，问：小球运动到悬点的正下方B点时，悬线中的张力为多大？
（2012?昌平区二模）如图所示，用长为L的绝缘细线悬挂一带电小球，小球的质量为m、电荷量为q．现加一水平向左的匀强电场，平衡时小球静止于M点，细线与竖直方向成θ角．
如图所示，用长为L的细绳拴着质量为m的小球在竖直平面内做圆周运动，则下列说法中正确的是（ ）A、若小球刚好能在竖直平面内做圆周运动，则在最高点的速率为
| ||
| B、小球在最高点时绳子的拉力不可能为零 | ||
| C、小球在圆周最高点时所受的向心力一定为重力 | ||
| D、小球过最低点时绳子的拉力一定小于小球重力 |