题目内容
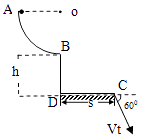
【题目】汽车过拱桥时速度过大会造成车辆失控,如图一辆质量为 1000kg 的汽车正通过一座半径为40m 的圆弧形拱桥顶部.求:(g取10m/s2)![]()
(1)汽车以多大速度v1通过拱桥的顶部时,拱桥对汽车的支持力恰好为零?
(2)如果汽车以v2=10m/s的速度经过拱桥的顶部,则拱桥对汽车的支持力是多大?
【答案】
(1)解:在拱桥顶部,由牛顿第二定律有:
![]()
解得:v1=20m/s
答:汽车以20m/s的速度v1通过拱桥的顶部时,拱桥对汽车的支持力恰好为零
(2)解:设拱桥对汽车的支持力为FN,由牛顿第二定律有:
![]()
解得:FN=7500N
答:如果汽车以v2=10m/s的速度经过拱桥的顶部,则拱桥对汽车的支持力是7500N
【解析】(1)汽车在拱桥顶部支持力等于0时,重力提供向心力。
(2)汽车过拱桥顶部时重力和支持力的合力提供向心力。
【考点精析】解答此题的关键在于理解向心力的相关知识,掌握向心力总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小;向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时,千万不可在物体受力之外再添加一个向心力.

练习册系列答案
相关题目