��Ŀ����
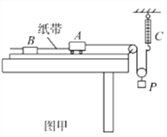
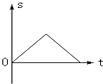
����Ŀ��ͼ1Ϊ��֤ţ�ٵڶ����ɵ�ʵ��װ��ʾ��ͼ��ͼ�д���ʱ���ĵ�ԴΪ50Hz�Ľ�����Դ������ʱ�����á�t��ʾ����С������δ֪������£�ijͬѧ�����һ�ַ��������о���������һ���������£�����ļ��ٶ�����������Ĺ�ϵ����
��1���������ʵ�鲽���е���գ�
��ƽ��С�����ܵ�������С�����в�����飬����ľ���Ҷ˵ĸ߶ȣ������ᲦС����ֱ������ʱ�����һϵ���ĵ㣮
�ڰ�סС������С�����з����ʵ���������飬��С���з������룮
�۴���ʱ����Դ���ͷ�С������ô��е��е�ֽ������ֽ���ϱ��С�������������m��
�ܰ�סС�����ı�С����������������ظ�����ۣ�
����ÿ��ֽ���������IJ��֣�û5�������עһ�������㣮�������ڼ�����ļ��s1 �� s2 �� ��������벻ͬm���Ӧ�ļ��ٶ�a��
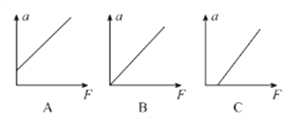
�������������mΪ������1/aΪ�����꣬������ֽ������1/a��m��ϵͼ�ߣ������ٶ���С����������������ɷ��ȣ���1/a��m��Ӧ����ϵ������ԡ������ԡ�����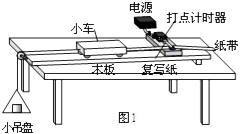
��2�����������գ�
����ʵ���У�Ϊ�˱�֤�ڸı�С�������������ʱ��С�����ܵ��������Ʋ��䣬С���̺�������������֮��Ӧ����������� ��
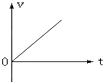
����ͼ2Ϊ����ʵ��ͼ�ߵ�ʾ��ͼ����ͼ��ֱ�ߵ�б��Ϊk���������ϵĽؾ�Ϊb����ţ�ٶ��ɳ�������С���ܵ�������Ϊ �� С��������Ϊ �� 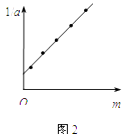
���𰸡�
��1���������,����
��2��ԶС��С���������������,![]() ,
,![]()
���������⣺��1����ƽ��Ħ�����ı�ΪС�����������˶�������ʱ�������ֽ���㼣������ȣ����Դ��ǣ�������Ȣ���a= ![]() ����
���� ![]() =
= ![]() a���ʳ����Թ�ϵ�����Դ��ǣ����ԣ�2��
a���ʳ����Թ�ϵ�����Դ��ǣ����ԣ�2��
������С��������ΪM��С���̺�������������Ϊm��������������ΪF��
������Ϊ�о�������mg=��m+M��a
���a= ![]() ��MΪ�о����������ӵ�����F=Ma=
��MΪ�о����������ӵ�����F=Ma= ![]() mg
mg
��ȻҪ��F=mg����m+M=M������M����m����ֻ��M����mʱ�ſ�����Ϊ����С����������С����С���̺�������������������Ϊ�˱�֤�ڸı�С�������������ʱ��С�����ܵ��������Ʋ��䣬С���̺�������������֮��Ӧ��ԶС��С��������������������Դ��ǣ�ԶС��С���������������������С������ΪM��С���ܵ�����ΪF����ţ�ٵڶ�������F=��m+M��a��
���ԣ� ![]() =
= ![]() +
+ ![]()
���ԣ� ![]() ��mͼ���б��Ϊ
��mͼ���б��Ϊ ![]() ����F=
����F= ![]() ������ؾ�Ϊb=
������ؾ�Ϊb= ![]() =kM��
=kM��
���ԣ�M= ![]()
���Դ��ǣ���1���ټ�����Ȣ����ԣ�2������ԶС��С������������������� ![]() ��
�� ![]()

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�