题目内容
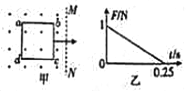
【题目】如图甲所示，一质量为M的长木板静置于光滑水平面上，上面放一质量为m的滑块。t=0时刻，滑块受到水平向右的拉力F随时间t的变化规律为F=kt，其中k=2N/s，用传感器测出滑块加速度a，得到的a-F图象如图乙所示。设滑块与木板之间的最大静摩擦力等于滑动摩擦力，g取10m/s2，下列判断正确的是
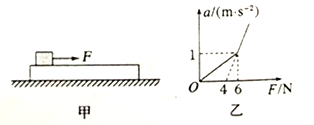
A. 滑块的质量等于0.5kg
B. 滑块与木板保持相对静止的时间为3s
C. 滑块与木板之间的动摩擦因数为0.2
D. 拉力等于6N时木板的速度为1.5m/s
【答案】BCD
【解析】当F等于6N时，加速度为： 
，对整体分析，由牛顿第二定律有： 
，解得： 
；当F大于6N时，对于滑块，根据牛顿第二定律得： 
，解得： 
，由图可知此时图线的斜率
，解得： 
，故A错误；由图可知，当F=6N时，滑块与木板将由相对静止到相对滑动，根据
，得：滑块与木板保持相对静止的时间为
，故B正确；根据F大于6N的图线知，F=4N时，a=0，即： 
，解得： 
，故C正确；当
时，滑块与木板相对静止，对整体分析，由牛顿第二定律有： 
，解得： 
，则作出a—t图如图所示：
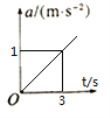
由题可知，经t=3s时拉力F=6N，此时加速度为
，在a—t图中图线与t轴围成的面积表示速度，故当F=6N时的速度为
，故D正确；选BCD.
练习册系列答案
阅读快车系列答案
相关题目
