题目内容
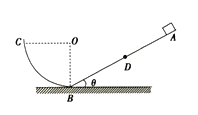
【题目】如图所示，倾角
、长
的斜面，其底端与一个光滑的
圆弧轨道平滑连接，圆弧轨道底端切线水平，一质量
的物块（可视为质点）从斜面最高点
由静止开始沿斜面下滑，经过斜面底端
后恰好能到达圆弧轨道最高点
，又从圆弧轨道滑回，能上升到斜面上的
点，再由点从斜面下滑沿圆弧轨道上升，再滑回，这样往复运动，物块最后停在点。已知物块与斜面间的动摩擦因数
，
，
，
，物块经过斜面与圆弧轨道平滑连接处无机械能损失
(1)物块经多长时间第一次到达点；
(2)求物块第一次经过圆弧轨道的最低点时对圆弧轨道的压力；
(3)求物块在斜面上滑行的总路程。
【答案】(1)3s；(2)30N，方向竖直向下；(3)13.5m
【解析】
(1)物块沿斜面下滑时，有
解得
从
点运动到
点，物块做匀加速运动，有
解得
(2)因为物块恰好到达
点，所以到达点的速度为0，设物块到达点的速度为
，则有
解得
由牛顿第三定律可得，物块对圆弧轨道的压力
方向竖直向下。
(3)从开始释放至最终停在处，设物块在斜面上滑行的总路程为
，则有
解得
练习册系列答案
相关题目
